Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì dao động con lắc lò xo:
\(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,4}{200}}=\dfrac{\pi\sqrt{5}}{25}\left(s\right)\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{\pi\sqrt{5}}{25}}=10\sqrt{5}\left(rad\right)\)
Biên độ dao động:
\(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{2^2+\dfrac{\left(20\sqrt{2}\right)^2}{\left(10\sqrt{5}\right)^2}}=\dfrac{2\sqrt{35}}{5}\approx2,4\left(cm\right)\)
Gốc thời gian là lúc vật ở VTCB nên \(\varphi_0=0\)
PT dao động:
\(x=Acos\left(\omega t+\varphi_0\right)=2,4cos\left(10\sqrt{5}t\right)\) (cm)

Vận tốc của vật vào thời điểm đó là: \(v=A\omega=\dfrac{2\pi A}{T}=\dfrac{2\pi\cdot10}{2}=10\pi\left(cm/s\right)\)

Câu 1.
a)Tốc độ góc: \(\omega=2\pi f=2\pi\)
Ta có: \(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{0,05^2+\dfrac{\left(0,10\pi\right)^2}{\left(2\pi\right)^2}}=\dfrac{\sqrt{2}}{20}m\)
b)Phương trình vận tốc:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-2\pi\cdot\dfrac{\sqrt{2}}{20}sin\left(2\pi t\right)\)
Câu 2.
a)Chu kỳ: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
b)Li độ tại thời điểm \(t=2s:\)
\(x=2cos\left(5\pi t+\dfrac{\pi}{3}\right)=2cos\left(5\pi\cdot2+\dfrac{\pi}{3}\right)=1\)

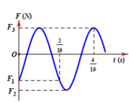
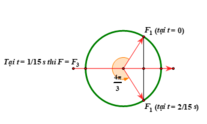


a)Chu kì: \(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,2}{200}}=0,2s\Rightarrow\omega=\dfrac{2\pi}{T}=10\pi\)
Vật qua vị trí \(x=1,5=\dfrac{A}{2}\) theo chiều dương nên \(\varphi=-\dfrac{\pi}{3}\).
PT dao động của vật: \(x=Acos\left(\omega t+\varphi\right)=3cos\left(10\pi-\dfrac{\pi}{3}\right)\left(cm\right)\)
b)Tại \(t=1s\) thì:
Vận tốc vật:
\(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi\cdot3\cdot sin\left(10\pi t-\dfrac{\pi}{3}\right)=-30\pi sin\left(10\pi t-\dfrac{\pi}{3}\right)\)
\(\Rightarrow v=-30\pi sin\left(10\pi\cdot1-\dfrac{\pi}{3}\right)\approx81,62cm/s\)
Gia tốc vật:
\(a=-\omega^2Acos\left(\omega t+\varphi\right)=-3000cos\left(10\pi t-\dfrac{\pi}{3}\right)\left(cm/s^2\right)\)
\(\Rightarrow a=-3000cos\left(10\pi\cdot1-\dfrac{\pi}{3}\right)=-1500\left(cm/s^2\right)\)