Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
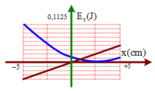
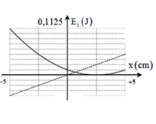
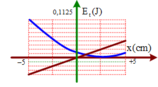
Từ hình vẽ : A = 5 cm
Vị trí lò xo không biến dạng có Δℓ = 0 → Etdh = 0 → x = 2,5 cm (trên hình)
Thang chia trên trục tung: 9 khoảng = 0,1125 J → 4 khoảng = 0,05J = Et hd max
Ta có: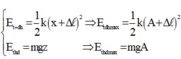


Áp dụng biểu thức độc lập, tốc độ của vật khi qua vị trí lò xo không biến dạng:
![]()

Chọn đáp án A
@ Lời giải:
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → Ehd = mgx → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
Edh = 0,5k(Δl0 – x)2 → ứng với đường nét liền.
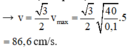
+ Từ đồ thị, ta có: xmax = A = 5 cm; Edhmax = mgA ↔ 0,05 = m.10.0,05 → m = 0,1 kg.
Edhmax = 0,5k(Δl + A)2 ↔ 0,1125 = 0,5.k(0,025 + 0,05)2 → k = 40 N/m.
+ Khi vật đi qua vị trí lò xo không biến dạng → x = Δl0 = 0,5A = 2,5 cm.
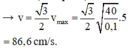

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Chọn đáp án A
@ Lời giải:
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → E h d = m g x → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
E d h = 0 , 5 k ( Δ l 0 – x ) 2 → ứng với đường nét liền.
+ Từ đồ thị, ta có: x m a x = A = 5 c m ; E d h m a x = m g A ↔ 0 , 05 = m . 10 . 0 , 05 → m = 0,1 kg.
E d h m a x = 0 , 5 k ( Δ l + A ) 2 ↔ 0 , 1125 = 0 , 5 . k ( 0 , 025 + 0 , 05 ) 2 → k = 40 N/m.
+ Khi vật đi qua vị trí lò xo không biến dạng → x = Δ l 0 = 0 , 5 A = 2 , 5 c m .
→ v = 3 2 v m a x = 3 2 40 0 , 1 .5 = 86 , 6 cm/s.