

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án A
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → E h d = m g x → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
E d h = 0 , 5 k ( Δ l 0 – x ) 2 → ứng với đường nét liền
Từ đồ thị, ta có:
x m a x = A = 5 c m ; E d h m a x = m g A ↔ 0 , 05 = m . 10 . 0 , 05 → m = 0 , 1 k g
E d h m a x = 0 , 5 k ( Δ l + A ) 2 ↔ 0 , 1125 = 0 , 5 . k ( 0 , 025 + 0 , 05 ) 2 → k = 40 N / m
Khi vật đi qua vị trí lò xo không biến dạng → x = Δ l 0 = 0 , 5 A = 2 , 5 c m
→ v = 3 2 v m a x = 3 2 40 0 , 1 .5 = 86 , 6 c m / s

Đáp án A
Từ hình vẽ : A = 5 c m
Vị trí lò xo không biến dạng có Δ ℓ = 0 → E t d h = 0 → x = 2 , 5 c m (trên hình)
Thang chia trên trục tung: 9 k h o ả n g = 0 , 1125 J → 4 k h o ả n g = 0 , 05 J = E t h d m a x
Ta có:
E t + d h = 1 2 k x + Δ l 2 ⇒ E t d h m ax = 1 2 k A + Δ l 2 ⇔ 0,1125 = 1 2 k 0,05 + 0,025 2 ⇒ k = 40 N / m E t h d = m g z ⇒ E t h d m ax = m g A ⇔ 0,05 = m .10.0,05 ⇒ m = 0,1 k g
⇒ ω = 40 0,1 = 20 r a d / s
Áp dụng biểu thức độc lập, tốc độ của vật khi qua vị trí lò xo không biến dạng:
v = ω A 2 − x 2 = 20 5 2 − 2,5 2 = 50 3 ≈ 86 , 6 c m / s

Chọn đáp án A
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên
→ Ehd = mgx
→ đường nét đứt ứng với đồ thị thế năng hấp dẫn.
![]() →
ứng với đường nét liền.
→
ứng với đường nét liền.
Từ đồ thị, ta có: xmax = A = 5 cm; Edhmax = mgA ↔ 0,05 = m.10.0,05 → m = 0,1 kg.
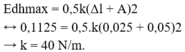
Khi vật đi qua vị trí lò xo không biến dạng
→
![]()
→
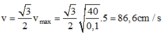

Đáp án D
+ Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật vật đi qua vị trí có li độ x = 5 3 cm l
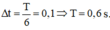
+ Lực kéo cực đại của lò xo tác dụng và điểm có định là
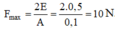
+ Vậy khoảng thời gian ngắn nhất để lò xo kéo điểm cố định một lực 5 N là
![]()