Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(T=2\pi\sqrt{\dfrac{l}{g}}\\ \Rightarrow g=\dfrac{4\pi^2\cdot l}{T^2}=1,6m/s^2\)

a) Chu kì và tần số góc của con lắc.
Chu kì T = 1,2 s
Tần số góc là:
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{1,2}=5,24\left(rad/s\right)\)
b) Vận tốc cực đại của vật.
Theo đồ thì biết biên độ A = 0,35
\(v_{max}=0,35\left(m/s\right)\)
c) Cơ năng của con lắc.
\(W=\dfrac{1}{2}mv_{max}^2=\dfrac{1}{2}\cdot0,2\cdot0,35^2=0,012\left(J\right)\)
d) Biên độ của vật.
\(A=\dfrac{v_{max}}{\omega}=\dfrac{0,35}{5,24}=0,067\left(m\right)\)

Những con lắc khác cũng dao động do hiện tượng cộng hưởng, mỗi con lắc dao động với tần số khác nhau.
Con lắc dao động mạnh nhất là con lắc có chu kì gần nhất với chu kì dao động của con lắc, mặc khác chu kì dao động của các con lắc đơn lại tỉ lệ với chiều dài → con lắc có chiều dài gần nhất với chiều dài của con lắc do đó sẽ dao động với biên độ lớn nhất.

a) Cơ năng bằng động năng cực đại:
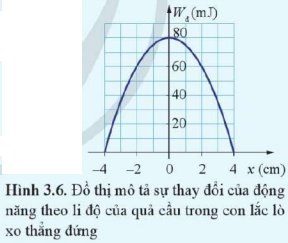
\(W=W_{đmax}=80\left(mJ\right)=80\cdot10^{-3}\left(J\right)\)
b) Ta có:
\(W_{đmax}=80\cdot10^{-3}\left(J\right)\Rightarrow80\cdot10^{-3}\left(J\right)=\dfrac{1}{2}\cdot0,4\cdot v^2_{max}\)
\(\Rightarrow v_{max}=\sqrt{\dfrac{80\cdot10^{-3}}{\dfrac{1}{2}\cdot0,4}}=\dfrac{\sqrt{10}}{5}\left(m/s\right)\)
c) Khi li độ bằng 2 cm thì dựa vào đồ thị ta thấy động năng có giá trị là Wđ = 60 mJ.
Thế năng tại vị trí đó:
\(W_t=W-W_đ=80-60=20\left(mJ\right)=20\cdot10^{-3}\left(J\right)\)

tham khảo
Ta biết chu kì con lắc đơn không phụ thuộc vào khối lượng của vật (vì \(T=2\pi\sqrt{\dfrac{1}{g}}\)).
Mà \(T=\dfrac{2\pi}{\omega}\) nên tần số góc \(\omega\) không phụ thuộc vào khối lượng của vật. Bên cạnh đó bài toán giữ nguyên biên độ của dao động cho nên vận tốc khi qua vị trí cân bằng không đổi, tức là trong cả hai trường hợp vận tốc qua vị trí cân bằng giống nhau.
Suy ra nhận định trên là sai.



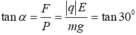
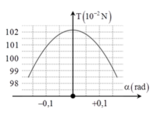
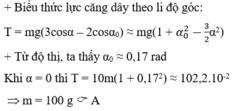

- Con lắc chuyển động nên nó có động năng.
- Khi con lắc chuyển động, nó có sự thay đổi độ cao so với mốc tính thế năng (giả sử chọn ở VTCB) nên nó có thế năng.