Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+Khi có lực lạ gia tốc trọng trường biểu kiến 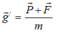
Trong trường hợp cụ thể:
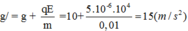
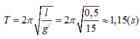

a 30
\(\omega =4\pi(rad/s)\)
\(|a|\le160\sqrt 3\) ứng với phần gạch đỏ trên hình, thời gian 1/3T ứng với véc tơ quay 1 góc 1200,.
Do vậy, mỗi một góc nhỏ là 300
\(\Rightarrow a_{max}=\dfrac{a}{\sin 30^0}=2a=320\sqrt 3(cm/s) \)
\(\Rightarrow A = \dfrac{a_{max}}{\omega^2}=2\sqrt 3(cm)\)
Cơ năng: \(W=\dfrac{1}{2}kA^2\Rightarrow k=\dfrac{2W}{A^2}=\dfrac{0,004}{(0,02\sqrt 3)^2}=...\)

Chu kỳ dao động của con lắc
$T=2\pi\sqrt\frac{l}{g}$
Khi đặt trong điện trường và con lắc mang điện tích thì vật còn chịu thêm lực điện
Gia tốc tương đối có thể biểu diễn bằng g'
Qua so sánh 2 giá trị chu kỳ thì ta thấy trong trường hợp đầu sẽ có gia tốc tương đối lớn hơn
$g'_{1}=g+\frac{Eq}{m}=g+a$ đặt a, q dương
$g'_{2}=g-a$
Ta có biểu thức
$T_{1}^{2}g'_{1}=T_{2}^{2}g'_{2}=4\pi^{2}l=T^{2}g$
$g'_{1}+g'_{2}=g+a+g-a=2g=\frac{T^{2}g}{T_{1}^{2}}+\frac{T^{2}g}{T_{2}^{2}}$
$2=T^{2}(\frac{1}{T_{1}^{2}}+\frac{1}{T_{1}^{2}})$<br><br>$T\approx 1.9058s$

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.


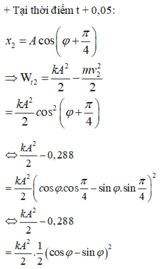


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D




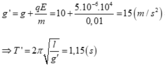
Đáp án C
Lực điện: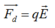
Các lực tác dụng vào vật:
Cường độ điện trường: E = U/d = 80/0,2 = 400 (V/m)
Độ lớn lực tổng hợp tác dụng vào hòn bi:
=> Chu kì