Bài 3: Một con lắc đơn có chiều dài dây treo 1 m, dao động điều hòa tại nơi có gia tốc trọng trường g π2 m/s2.Số lần động năng bằng thế năng trong khoảng thời gian 4 s là A. 16. B. 6. C. 4. D. 8.Bài 4: Một vật dao động điều hoà theo phương trình x = 2cos(5πt -π/3) (cm) (t đo bằng giây).Trong khoảng thời gian từ t = 1 (s) đến t = 2 (s) vật đi qua vị trí x = 0 cm được mấy lần? A. 6 lần. B. 5 lần. C. 4...
Đọc tiếp
Bài 3: Một con lắc đơn có chiều dài dây treo 1 m, dao động điều hòa tại nơi có gia tốc trọng trường g π2 m/s2.
Số lần động năng bằng thế năng trong khoảng thời gian 4 s là A. 16. B. 6. C. 4. D. 8.
Bài 4: Một vật dao động điều hoà theo phương trình x = 2cos(5πt -π/3) (cm) (t đo bằng giây).
Trong khoảng thời gian từ t = 1 (s) đến t = 2 (s) vật đi qua vị trí x = 0 cm được mấy lần? A. 6 lần. B. 5 lần. C. 4 lần. D. 7 lần. Bài 5: Một chất điểm dao động điều hòa theo phương trình x = Acos(2πt/T + π/4) (cm). Trong khoảng thời gian 2,5T đầu tiên từ thời điểm t = 0, chất điểm đi qua vị trí có li độ x = 2A/3 là A. 9 lần. B. 6 lần. C. 4 lần. D. 5 lần.
Bài 6: Một chất điểm dao động điều hoà có vận tốc bằng không tại hai thời điểm liên tiếp là t1 = 2,2 (s) và t2 = 2,9 (s). Tính từ thời điểm ban đầu (to = 0 s) đến thời điểm t2 chất điểm đã đi qua vị trí cân bằng A. 9 lần. B. 6 lần. C. 4 lần. D. 5 lần
. Bài 7: Một vật dao động điều hoà theo phương trình: x = 2cos(5πt - π/3) (cm). Trong giây đầu tiên kể từ lúc bắt đầu dao động vật đi qua vị trí có li độ x = -1 cm theo chiều dương được mấy lần? A. 2 lần. B. 3 lần. C. 4 lần. D. 5 lần.
Bài 8: Một chất điểm dao động điều hoà tuân theo quy luật: x = 5cos(5πt - π/3) (cm). Trong khoảng thời gian t = 2,75T (T là chu kì dao động) chất điểm đi qua vị trí cân bằng của nó A. 3 lần. B. 4 lần. C. 5 lần. D. 6 lần.
Bài 9: Một chất điểm dao động điều hòa với phương trình: x = 4cos(4πt + π/3) (cm). Trong thời gian 1,25 s tính từ thời điểm t = 0, vật đi qua vị trí có li độ x = -1 cm A. 3 lần. B. 4 lần. C. 5 lần. D. 6 lần. Bài 10: Chất điểm dao động điều hòa với phương trình: x = Acos(2πt/T + π/4) (cm). Trong thời gian 2,5T kể từ thời điểm t = 0, số lần vật đi qua li độ x = 2A/3 làπ A. 6 lần. B. 4 lần. C. 5 lần. D. 9 lần.



Với biên độ góc là 600 vẽ hình sẽ thấy độ cao


 =2 7,1 cm/s
=2 7,1 cm/s
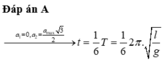
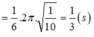
Đáp án C