Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sự tổ hợp giữa hai gen tạo ra 3 kiểu gen: AA, aa, Aa.
b) Khi giao phối ngẫu nhiên, ta lấy 2 gene bất kì trong 3 kiểu gene kết hợp với nhau
Khi đó, các kiểu giao phối khác nhau được tạo ra từ 3 kiểu gene trên là:
AA x AA; AA x Aa; AA x aa; Aa x Aa; Aa x aa; aa x aa
=> Có 6 kiểu giao phối khác nhau

Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)

a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
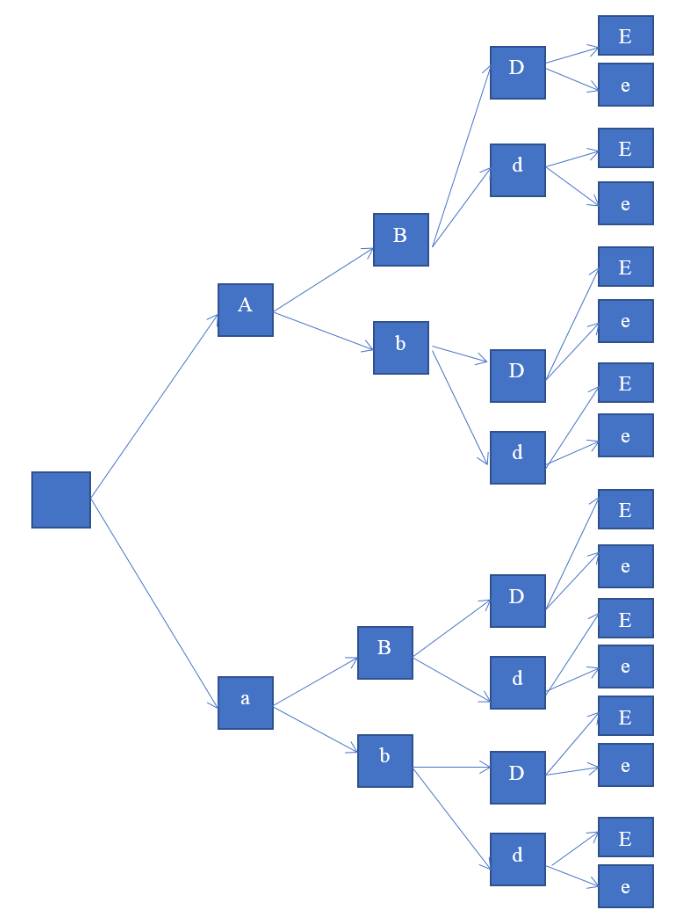
b) Dựa vào sơ đồ cây, số loại giao từ cua kiểu gen AaBbDdEe là: 16 (loại)

1 tế bào tiến hành giảm phân tạo ra 1 trứng và 3 thể cực
30 tế bào tiến hành giảm phân tạo ra 30 trứng và 90 thể cực.

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)

Để cho dễ tính toán, ta coi như việc chọn 2 số là theo thứ tự
Không gian mẫu: \(A_{90}^2\)
Chọn số thứ nhất: \(C_{90}^1=90\) cách
Hàng đơn vị số thứ 2 có 1 cách chọn (giống hàng đơn vị số thứ nhất), hàng chục số thứ 2 có 8 cách chọn (khác hàng chục số thứ hai và 0)
\(\Rightarrow90.1.8\) cách chọn 2 số thỏa mãn yêu cầu
Xác suất: \(P=\dfrac{90.1.8}{A_{90}^2}\)

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 3 của 4 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_4^3\) ( phần tử)
b) +) Sự kiện “Tổng các số trên ba tấm bìa bằng 9” tương ứng với biến cố \(A = \left\{ {\left( {4;3;2} \right)} \right\}\)
+) Sự kiện “Các số trên ba tấm bìa là ba số tự nhiên liên tiếp” tương ứng với biến cố \(B = \left\{ {\left( {1;2;3} \right),\left( {2;3;4} \right)} \right\}\)
c) +) Ta có: \(n\left( A \right) = 1\),\(n\left( B \right) = 2\)
+) Vậy xác suất của biến cố A và B là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

a: n(omega)=40
n(A)=20
=>P(A)=20/40=1/2
b: B={3;6;..;39}
=>n(B)=13
=>P(B)=13/40
Tổng số giao tử được tạo ra sau khi giảm phân là \(n\left( \Omega \right) = {2^8}\)
Giao tử được chọn mang đầy đủ các alen trội khi giao tử có kiểu gen luôn có các alen A, B, D, E
Số kết quả thuận lợi cho việc chọn giao tử mang đầy đủ gen trội là \(n = 1.2.1.2.1.2.1.2 = {2^4}\)
Suy ra xác suất để giao tử được chọn mang đầy đủ các alen trội là \(P = \frac{{{2^4}}}{{{2^8}}} = \frac{1}{{16}}\)