Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

Đáp án A
+ Chu kì dao động của con lắc khi không có và có điện trường:
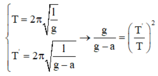
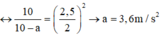

Đáp án D
+ Chu kì dao động của con lắc T = π l g + π 0 , 5 l g = π 1 π 2 + π 0 , 5 π 2 = 1 + 2 2 s

mk nghĩ làm bài này như sau:
Ta có:\(\begin{cases}T1=2\pi\sqrt{\frac{l1}{g}}\\T2=2\pi\sqrt{\frac{l2}{g}}\end{cases}\)\(\Rightarrow\sqrt{\frac{l1.l2}{g^2}}=\frac{T1.T2}{\left(2\pi\right)^2}\)\(\Rightarrow\frac{1}{\sqrt{g}}.\sqrt{\frac{l1.l2}{g}}=\frac{T1.T2}{\left(2\pi\right)^2}\)
\(\Rightarrow\) \(T3=2\pi\sqrt{\frac{l1.l2}{g}}=\frac{\sqrt{g}}{2\pi}T1.T2\)
Chọn C

Đáp án B
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn T = 2 π l g
Cách giải:
Khi gia tốc trọng trường giảm 4,5 lần, chiều dài dây treo giảm 2 lần thì:
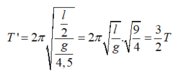
Vậy chu kì tăng lên 1,5 lần

Đáp án D
Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn T = 2 π l g
Cách giải:
Công thức tính chu kì dao động của con lắc đơn T = 2 π l g => Chu kì sóng tỉ lệ thuận với l
=> Khi chiều dài dây giảm 2 lần thì chu kì giảm 2 lần
=> T ' = T 2 => Chọn D