Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Vật sẽ dừng lại khi rơi vào khoảng O1OO2 ( O1, O2 là các vị trí mà lực đàn hồi cân bằng với lực ma sát, OO1 = OO2 = μmg/k = 5.10-4m (rất nhỏ) nên trong khoảng O1OO2 ta có thể bỏ qua thế năng đàn hồi của lò xo khi áp dụng định luật bảo toàn năng lượng.
+ Gọi S là tổng quãng đường vật đã đi được thì toàn bộ năng lượng ban đầu của con lắc lò xo biến thành công của lực ma sát:
![]()
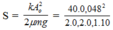
![]()

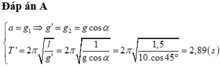
Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos a\)
Chu kì dao động: \(T=2\pi\sqrt{\frac{l}{g'}}=2\pi\sqrt{\frac{1,5}{10.\cos45^o}}\approx2,89\left(s\right)\)

Toa xe trượt không ma sát trên đường dốc với góc nghiêng \(\alpha\)
Ta có kết quả:
+ Khi vật ở VTCB thì phương của sợi dây vuông góc với mặt phẳng nghiêng.
+ Gia tốc hiệu dụng của vật: \(g'=g.\cos\alpha\)
Chu kì dao động: \(T=2\pi\sqrt{\dfrac{\ell}{g'}}=2\pi\sqrt{\dfrac{1,5}{10.\cos 45^0}}\approx2,89(s)\)

Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
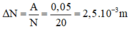
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB:
![]()

Chọn C

+ Độ giảm biên độ trong nửa chu kì: ![]()
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn: ![]()
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.