Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2p=120s\)
\(v=\dfrac{\Delta s}{\Delta t}=\dfrac{2\pi100}{120}=5,23\left(\dfrac{m}{s}\right)\)
2 phút=120s
=>T= 120=>ω=\(\dfrac{2\pi}{T}\)=\(\dfrac{\pi}{60}\)
=>\(\nu\)=R.ω=100.\(\pi\)

Chạy một vòng hết 20s=> Chu kỳ của điểm nằm trên xe là: 20(s)
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{20}=\dfrac{\pi}{10}\left(s\right)\)
Rồi cho bán kính để gây nhiễu mắt hở :v?

Gia tốc hướng tâm:
\(a_{ht}=\dfrac{v^2}{r}=r\cdot\omega^2=100\cdot2^2=400\)m/s2

Khi xe đạp chuyển động thẳng đều, một điểm M trên vành bánh xe đối với người quan sát ngồi trên xe chỉ chuyển động tròn đều. (Đối với mặt đất, điểm M còn tham gia chuyển động tịnh tiến) khi đó tốc độ dài của M bằng tốc độ dài của xe :

Đáp án D
Trong 2 phút 20 giây người đó chạy được
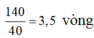
Vậy quãng đường người đó chạy được
![]()

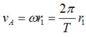
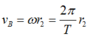
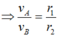
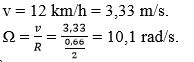
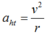
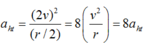
1 vòng hết 2 phút = 120s
=> T = 120 (s)
Tốc độ dài của xe: v=Δs/Δt
Khi quay hết một vòng ta có: Δs=2πR;Δt=T
Ta suy ra: v=2πRT=2.3,14.100120=5,23m/s