Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
23² + 40² = 2129
Độ dài đường chéo màn hình:
√2129 : 2,54 ≈ 18,2 (inch)

Gọi chiều dài, chiều rộng lần lượt là a(inch) và b(inch)
Chiều dài, chiều rộng lần lượt tỉ lệ với 16 và 9 nên a/16=b/9
Đặt \(\dfrac{a}{16}=\dfrac{b}{9}=k\)
=>a=16k; b=9k
Kích thước đường chéo là 55inch nên \(a^2+b^2=55^2\)
=>\(\left(16k\right)^2+\left(9k\right)^2=55^2\)
=>\(256k^2+81k^2=55^2\)
=>\(k^2=\dfrac{3025}{337}\)
=>\(k=\dfrac{55}{\sqrt{337}}\)
=>\(a=16\cdot\dfrac{55}{\sqrt{337}}=\dfrac{880}{\sqrt{337}};b=9\cdot\dfrac{55}{\sqrt{337}}=\dfrac{495}{\sqrt{337}}\)
=>\(a=\dfrac{880}{\sqrt{337}}inch\simeq121,76\left(cm\right)\)
\(b=\dfrac{495}{\sqrt{337}}inch=68,49\left(cm\right)\)

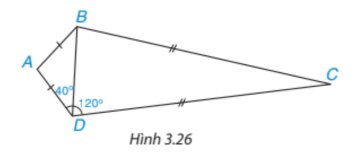
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

* Hình chữ nhật có:
- Hai cạnh đối song song và bằng nhau.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
* Dâu hiệu nhận biết hình chữ nhật:
- Hình bình hành có một góc vuông là hình chữ nhật.
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

a, Vì ti vi là hình chữ nhật nên đường chính là đường chéo của hình chữ nhật đó
Khi đó \({d^2} = \sqrt {74,{7^2} + {{32}^2}} \approx 81(cm)\)
Đổi 81cm = \( \frac {81} {2,54} \approx \) 32inch
b, Khoảng cách tối thiểu là:
\(5,08.32 = 162,56(cm) \approx 1,6m \)
Khoảng cách tối đa là:
\(7,62.32 = 243,84(cm) \approx 2,4m\)

link hình 1 đây nha mình nhầm:https://photos.app.goo.gl/qA8ev4JkVjLRaFNe7
hình 2 ko có, viết nhầm đề

a) Tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) (tổng các góc trong tứ giác ABCD)
Gọi \(x,y,z,t\) lần lượt là số đo các góc: \(\widehat{A},\widehat{B},\widehat{C},\widehat{D}\) \(\left(x,y,z,t>0\right)\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}=\dfrac{t}{4}=\dfrac{x+y+z+t}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)
\(\dfrac{y}{2}=36^0\Rightarrow y=2.36^0=72^0\) (nhận)
Vậy \(\widehat{B}=72^0\)
b) Đường chéo của màn hình điện thoại:
\(\sqrt{7^2+15,5^2}\simeq17\left(cm\right)\) \(\simeq17.2,54\simeq43\left(inch\right)\)

- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)




Độ dài đường chéo là:
\(\sqrt{72^2+120^2}=24\sqrt{34}\left(cm\right)\simeq55,1\left(inch\right)\)