Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau

Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)

a. Ta có: \(sin\left(30t\right)\le1\)
\(\Leftrightarrow3sin\left(30t\right)\le3\)
\(\Leftrightarrow5+3sin\left(30t\right)\le8\)
Vậy độ sâu mực nước lớn nhất tại bến cảng đó là 8(m)
b. Ta có: \(8\ge h\ge6,5\) \(\Leftrightarrow8\ge5+3sin\left(30t\right)\ge6,5\)\(\Leftrightarrow3\ge3sin\left(30t\right)\ge1,5\)
\(\Leftrightarrow1\ge sin\left(30t\right)\ge0,5\)\(\Leftrightarrow\dfrac{\pi}{2}\ge30t\ge\dfrac{\pi}{6}\)\(\Leftrightarrow\dfrac{\pi}{60}\ge t\ge\dfrac{\pi}{180}\)
Vậy sau giữa trưa từ \(\dfrac{\pi}{180}\) (giờ) đến \(\dfrac{\pi}{60}\)(giờ) thuyền có thể vào bến cảng

Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5 > 2\)
\( \Rightarrow f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5 > 0\)
Xét tam thức \(f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a = - 0,03 < 0\)
Ta có bảng xét dấu như sau
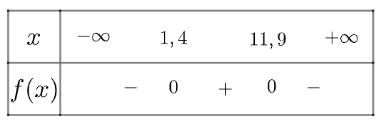
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét

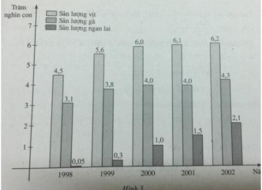
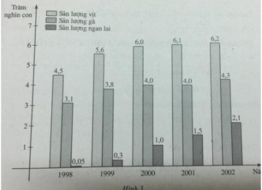
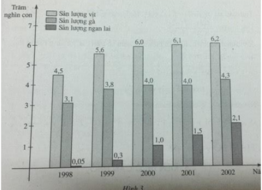
Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}

f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.

a)
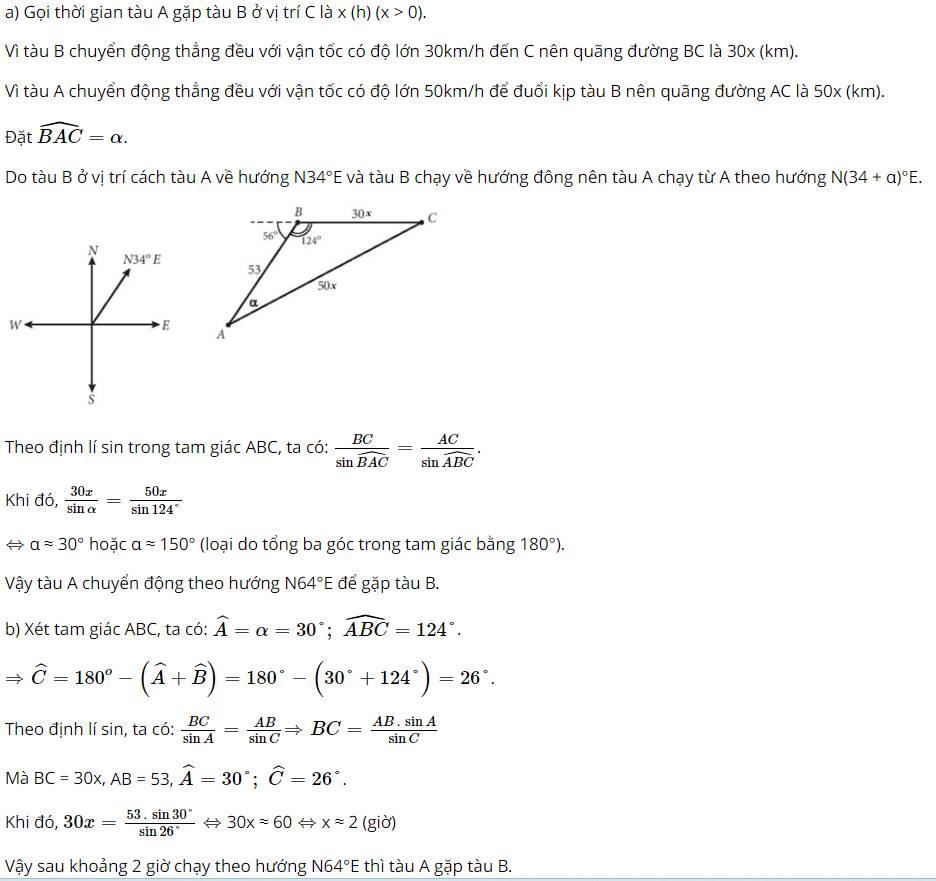
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

h(2002) - h(1999) = 210000 - 30000 = 180000 (con)
Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.