Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường xiên mà máy bay bay được :
\(600.\left(1,5:60\right)=15\left(km\right)\)
Sau 15 phút, máy bay bay được độ cao :
\(x=\sin30.15=7,5\left(km\right)\)
\(t=1,5\left(phút\right)=0,025\left(giờ\right)\)
Quãng đường bay sau \(0,025\left(giờ\right)\)
\(s=v.t=600.0,025=15\left(km\right)\)
Độ cao theo phương thẳng đứng là :
\(sin30^o=\dfrac{h}{s}\Rightarrow h=s.sin30^o=15.\dfrac{1}{2}=7,5\left(km\right)\)

\(1ph12s=\dfrac{1}{50}\left(h\right)\)
Độ dài đường bay máy bay bay được:
\(550.\dfrac{1}{50}=11\left(km\right)\)
Độ cao máy bay lên được theo phương đứng:
\(11.sin30^0=5,5\left(km\right)\)

Sau 3,6p=3/50h máy bay bay được:
500*3/50=30km
Độ cao của máy bay là:
30*sin30=15(km)

Lời giải:
Sau 2 phút bay máy bay đi được quãng đường:
$AC=600:60.2=20$ (km)
Đổi $20$ km = $20000$ m
Có: $\sin A = \frac{CB}{CA}=\frac{8500}{20000}=\frac{17}{40}$
$\Rightarrow \widehat{A}\approx 25,15^0$

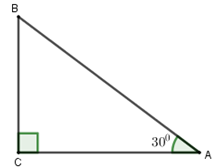
A B C 30 độ
Theo hình vẽ, áp dụng hệ thức lượng trong \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(\frac{BC}{AC}=sin\widehat{BAC}\Leftrightarrow AC=\frac{BC}{sin\widehat{ABC}}=\frac{BC}{sin30^o}=\frac{5}{\frac{1}{2}}=10km\)
Thời gian để máy bay đạt độ cao là 5km là:
\(t=\frac{s}{v}=\frac{10}{500}=0,02h=1,12'\)

 nha bạn chúc bạn học tốt nha
nha bạn chúc bạn học tốt nha