K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Lời giải:
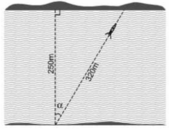
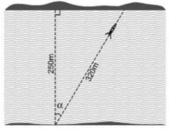
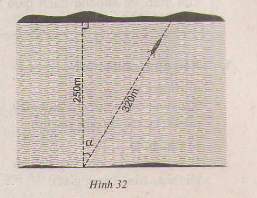
Giả sử dòng nước đẩy chiếc đò lệch đi một góc $\alpha$
Ta có: $\cos \alpha=\frac{250}{320}=\frac{25}{32}$
$\Rightarrow \alpha=38,62^0$

PN
4 tháng 10 2017
Chiếc đò lệch đi một góc bằng:
\(\cos\alpha=\frac{250}{320}\Rightarrow\alpha\approx38^o37'\)
4 tháng 10 2017
Chiếc đò lệch đi một góc bằng:
250/320=~38`37(sấp xỉ 38 độ 37)
ĐS:....(Tự điền nha)

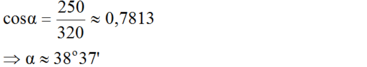
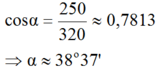

chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)