Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có:
thời gian đi từ A dến B là:
t1=t2/1,5=1h
do vận tốc tỉ lệ nghịch với thời gian nên:
\(\frac{v+v'}{v-v'}=\frac{t_2}{t_1}=1,5\)
\(\Leftrightarrow v+v'=1,5\left(v-v'\right)\)
\(\Leftrightarrow v+v'=1,5v-1,5v'\)
\(\Leftrightarrow0,5v-2,5v'=0\)
\(\Leftrightarrow0,5v=2,5v'\)
\(\Rightarrow v=5v'\)
ta lại có:
S1+S2=2S
\(\Leftrightarrow1\left(v+v'\right)+1,5\left(v-v'\right)=2.48\)
\(\Leftrightarrow v+v'+1,5v-1,5v'=96\)
\(\Leftrightarrow2,5v-0.5v'=96\)
mà v=5v' nên:
2,5.5v'-0.5v'=96
\(\Rightarrow12v'=96\)
giải phương trình ta có:
v'=8km/h;v=40km/h
vận tốc trung bình của canô trong một lượt đi về là:
\(v_{tb}=\frac{2S}{t_1+t_2}=\frac{48.2}{1.5+1}=\frac{96}{2.5}=38.4\)

Bài 1
a) Thời gian chuyển động của thuyền khi xuôi dòng là
tx=S/vt+vd=18/15+3=1h
Thời gian chuyển động của thuyền khi ngược dòng là
tn=S/vt-vd=18/15-3=1,5h
Thời gian chuyển động của thuyền là
t=tx+tn=1+1,5=2,5h
b) Trong 24p sửa máy, thuyền bị trôi quãng đường là
St=vd.ts=3.0.4=1,2 km
Vậy khi ngược dòng về A, thuyền phải đi trong thời gian là
t'n=SAB+St/vn=19,2/12=1,6h
Vậy thời gian chuyển động của thuyền là
t'=tx+t'n=1+1,6=2,6h
Bài 2
a)Trong thời gian sửa máy, thuyền bị trôi quãng đường là
St=vd.ts=5.0,2=1 km
QĐ mà thuyền đi vs vận tốc của nó là
S1=SAB-St=100-1=99km
Thuyền đi QĐ này trong
t1=s1/vx+vd=99/40=2,475h
Thời gian chuyển động của thuyền là
t=t1+ts=2,475+0,2=2,675=2h40p30s
b) Nếu thuyền ko phải sửa thì về đến nơi trong
t'=S/vt+vd=100/40=2,5h=2h30p

Gọi vận tốc của người đi xe đạp là x (km/giờ)
=> Vận tốc người đi xe máy là 4x
Thời gian người đi xe đạp đến B là 50/x
Thời gian người đi xe máy đến B là 40/x
Xe máy đến trước xe đáp :
1 + 1,5 = 2,5 (giờ)
Theo đề bài, ta có :
(50/x) - (50/4x) = 2,5
<=> 75/2x = 2,5 => x = 15 (km/giờ)
Vận tốc xe máy = 4x
=> Vận tốc xe máy = 15 . 4 = 60 (km/giờ)
bn ơi sao lại là 4x z
mk ko hiểu cho lắm bn có thể nói rõ cho mk hiểu một chút ko

Vận tốc tương đối của cano khi đi xuôi : vx=vtàu+vnước
Vận tốc tương đối của cano khi đi ngược : vn=vt-vn
Lập được phương trình thời gian cano đi xuôi và đi ngược :
\(\left\{{}\begin{matrix}t_x=\dfrac{AB}{v_x}\\t_n=\dfrac{AB}{v_n}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3=\dfrac{AB}{v_t+v_n}\\6=\dfrac{AB}{v_t-v_n}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=3\left(v_t+v_n\right)\\AB=6\left(v_t-v_n\right)\end{matrix}\right.\Leftrightarrow3\left(v_t+v_n\right)=6\left(v_t-v_n\right)\Leftrightarrow\left(v_t+v_n\right)=2v_t-2v_n\Leftrightarrow v_t=3v_n\)
Lập luận vận tốc bè xuôi chính là vận tốc của nước.
Nếu bè xuất phát cùng lúc với cano thì nó phải đi:
t'=\(\dfrac{AB}{v_n}\) (h) mà tx=\(\dfrac{AB}{v_x}=\dfrac{AB}{4v_n}\)=3 => t'= tx .4=3.4=12(h)
Chiếc bè đến B chậm hơn cano khoảng
t''=t'-tx=12-3=9(h)
Vậy....

a, Tgian đi hết sAB
\(t_1=\dfrac{s_{AB}}{v_1}=\dfrac{20}{5}=4h\)
Vì cứ 1h lại nghỉ 30p nên người đó nghỉ 3 lần
b, theo đề bài ta có chuyển động của người chở hàng
\(B\rightarrow A\rightarrow B\rightarrow A\)
=> Có nghĩa là đi 3 lần
Thời gian đi
\(t_2=\dfrac{s_{AB}}{v_2}=\dfrac{20.3}{20}=3h\)
Vì người chở hàng đi sAB ít hơn người đi bộ nên số lần bằng nhau cũng bằng số lượt xe chở hàng đi
Tham Khảo.
a. n1:t'=30(')=0,5(h)n1:t′=30(′)=0,5(h) ∣∣ t''=1(h)t′′=1(h)
Nếu người ấy đi không ngừng nghỉ, thì sẽ đến B sau:
t1=sv1=205=4(h)t1=sv1=205=4(h)
Vì người ấy bắt đầu xuất phát tại A, đến B thì dừng lại luôn nên số lần nghỉ là:
n=t1t'−1=41−1=3n=t1t′-1=41-1=3 (lần)
Tổng thời gian nghỉ là:
t2=n.t''=3.0,5=1,5(h)t2=n.t′′=3.0,5=1,5(h)
Tổng thời gian đi từ A đến B của người đi bộ là:
t3=t1+t2=4+1,5=5,5(h)t3=t1+t2=4+1,5=5,5(h)
b. Thời gian xe chở hàng đi hết quãng đường AB là:
t4=sv2=2020=1(h)t4=sv2=2020=1(h)
Nếu người đi bộ chỉ đi trong vòng 4 giờ đầu kể từ lúc xuất phát (5,5−0,5∣td=t3−tn)(5,5-0,5∣td=t3-tn), thì số lần gặp của người đi bộ với xe chở hàng là:
n2=tdt4=41=4n2=tdt4=41=4 (lần)
(số lần gặp cũng là số lần mà xe chở hàng đi từ A đến B)
Sau khi đi được 55 tiếng, xe chở hàng đứngở A : 1A−2b−3A−4B1A-2b-3A-4B
4=1+0,5+1+0,5+14=1+0,5+1+0,5+1 ⇒⇒ Nếu đi không ngừng nghỉ, quãng đương đi được của người đi bộ trong 3 tiếng tương đương với quãng đường người ấy đi trên thực tế (t_d +t_d +t_d=1+1+1=3)
Sau 44 tiếng người đi bộ đi được:
s1=v1.3=5.3=15(km)s1=v1.3=5.3=15(km)
Thời gian xe chở hàng và người đi bộ gặp nhau (TH* chuyển động không có điểm dừng, tính luôn người đi bộ chuyển động gặp xe chở hàng sau sau 4h)
tg=s1|v2+v1|=1520+5=0,6(h)tg=s1|v2+v1|=1520+5=0,6(h)
Khi ấy, người đi bộ đi được:
s2=v1.tg=5.0,6=3(km)s2=v1.tg=5.0,6=3(km)
⋅s<s1+s2=3+15=18(km)⋅s<s1+s2=3+15=18(km) ⇒⇒ Chửa đến AB
Điểm đó cách B một khoảng:
sB=s−(s1+s2)=20−18=2(km)sB=s-(s1+s2)=20-18=2(km)
Xe chở hàng đi được quãng đường kể từ khi gặp tại lần thứ 4:
s3=tg.v2=0,6.20=12(km)s3=tg.v2=0,6.20=12(km)
Nếu tính từ B, thì xe chở hàng kể từ lần thứ 4 gặp nhau đi được quãng đường cách B:
sB'=2+12=14(km)sB′=2+12=14(km)
Nhưng xe chở hàng còn phải về A, rồi từ A đến B với người đi bộ đến A trước khi gặp nhau lần thứ 5 (Giả thiết) nên không gặp thêm lần nữa, tức giả thiết không tồn tại | Tự chứng minh
(*Gợi ý: Khoảng cách tính từ A kể từ khi gặp nhau lần 4 đến khi người của người đi bộ luôn lớn hơn xe chở hàng)
Vậy Người đi bộ gặp người đi xe với số lần: n'=n3=4n′=n3=4(lần).

a) Số lần nghỉ của người đó là:
\(\dfrac{20}{5}-1=3\left(lần\right)\)
Thời gian người đó đến B là:
\(\dfrac{20}{5}+3.\dfrac{1}{2}=5,5\left(h\right)\)

gọi:
t là thời gian dự định
ta có:
nếu xe đi với vận tốc 48km/h thì:
\(t=\frac{S}{48}+0.3\)
nếu xe đi với vận tốc 12km/h thì:
\(t=\frac{S}{12}-0.45\)
do thời gian dự định ko đổi nên:
\(\frac{S}{48}+0.3=\frac{S}{12}-0.45\)
giải phương trình ta có S=12km
tứ đó ta suy ra t=0.55h
b)ta có:
AC+BC=12
\(\Leftrightarrow v_1t_1+v_2t_2=12\)
\(\Leftrightarrow48t_1+12t_2=12\)
mà t1+t2=t=0.55
\(\Rightarrow48t_1+12\left(0.55-t_1\right)=12\)
giải phương trình ta có: t1=0.15h
từ đó ta suy ra AC=7.2km

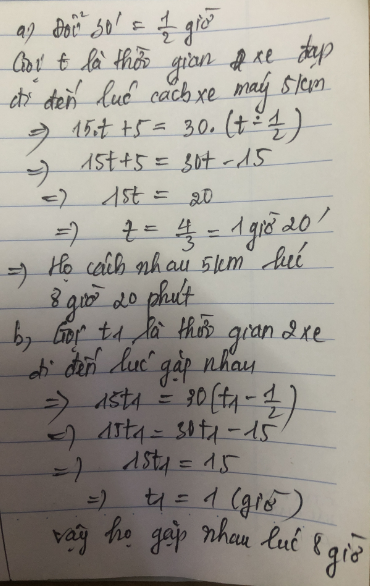
Tự tóm tắt ...........
-----------------------------------------------------------------------
Gọi vận tốc của ca nô và dòng nước tương ứng là \(v_1\) và \(v_2\)
Khi ca nô xuôi dòng thì : \(\dfrac{AB}{2}=v_1+v_2\left(1\right)\)
Khi ca nô ngược dòng thì \(:\dfrac{AB}{3}=v_1-v_2\left(2\right)\)
\(\left(1\right)-\left(2\right)=>\dfrac{AB}{2}-\dfrac{AB}{3}=2v_2\)
\(\Leftrightarrow3AB-2AB=2.12v_2\)
\(\Rightarrow AB=12v_2\)
Khi người đó tắt máy để ca nô trôi theo dòng nước mất :
\(t=\dfrac{AB}{2}=12\left(h\right)\)
Vậy ..................
Một chiếc canô đi xuôi dọc một con sông từ A đến B mất hất 2h \(\Rightarrow1h\) chiếc canô đó xuôi dòngđược:\(\dfrac{1}{2}\) dòng sông
Và canô đi ngược lại mất 3h\(\Rightarrow1h\) chiếc canô đó ngược dòng được:\(\dfrac{1}{3}\) dòng sông
1h canô trôi theo dòng nước được:
\(\left(\dfrac{1}{2}-\dfrac{1}{3}\right):2=\dfrac{1}{12}\) (dòng sông)
Vậy Canô trôi theo dòng nước hết:
\(1:\dfrac{1}{12}=12h\)