Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (m) là kích thước còn lại của hình chữ nhật
Điều kiện : x > 0
Ta có: 1,2x + π 0 , 6 2 = 2π 0 , 6 2
⇔ 1,2x = 2π 0 , 6 2 - π 0 , 6 2 =π0,36
⇔ 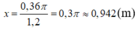
Vậy kích thước còn lại của hình chữ nhật phải là 0,942m

Gọi hình chữ nhật ban đầu là ABCDABCD có các cạnh AB=30cm,BC=20cmAB=30cm,BC=20cm.
Sau khi bớt mỗi cạnh của hình chữ nhật đi x(cm)x(cm), ta được hình chữ nhật mới là A′B′C′DA′B′C′D có các cạnh
A′B′=30−x(cm)A′B′=30−x(cm)
B′C′=20−x(cm)B′C′=20−x(cm)
Với yy là chu vi của hình chữ nhật A'B'C'D, ta có: y=2[(30−x)+(20−x)]y=2[(30−x)+(20−x)]
Rút gọn được y=−4x+100y=−4x+100.
Gọi hình chữ nhật ban đầu là ABCDABCD có các cạnh AB=30 cm, BC=20 cmAB=30cm,BC=20cm.
Sau khi bớt mỗi cạnh của hình chữ nhật đi x(cm)x(cm), ta được hình chữ nhật mới là A^{\prime} B^{\prime} C^{\prime} DA′B′C′D có các cạnh
A^{\prime} B^{\prime}=30-x(cm)A′B′=30−x(cm)
B^{\prime} C^{\prime}=20-x(cm)B′C′=20−x(cm)
Với yy là chu vi của hình chữ nhật A'B'C'D, ta có: y=2[(30-x)+(20-x)]y=2[(30−x)+(20−x)]
Rút gọn được y=-4 x+100y=−4x+100.

Bài 5: Gọi thời gian làm riêng của người thứ nhất và người thứ hai lần lượt là x(ngày) và y(ngày)
(Điều kiện: x>0; y>0)
Trong 1 ngày, người thứ nhất làm được: \(\frac{1}{x}\) (công việc)
Trong 1 ngày, người thứ hai làm được: \(\frac{1}{y}\) (công việc)
Trong 1 ngày, hai người làm được: \(\frac16\) (công việc)
Do đó, ta có: \(\frac{1}{x}+\frac{1}{y}=\frac16\left(1\right)\)
Trong 3 ngày, người thứ nhất làm được: \(\frac{3}{x}\) (công việc)
Trong 3+4=7 ngày, người thứ hai làm được: \(\frac{7}{y}\) (công việc)
Sau khi làm chung trong 3 ngày thì người thứ nhất đi làm việc khác, người thứ hai hoàn thành phần còn lại trong 4 ngày nên ta có: \(\frac{3}{x}+\frac{7}{y}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac16\\ \frac{3}{x}+\frac{7}{y}=1\end{cases}\Rightarrow\begin{cases}\frac{3}{x}+\frac{3}{y}=\frac36=\frac12\\ \frac{3}{x}+\frac{7}{y}=1\end{cases}\)
=>\(\begin{cases}\frac{3}{x}+\frac{7}{y}-\frac{3}{x}-\frac{3}{y}=1-\frac12=\frac12\\ \frac{1}{x}+\frac{1}{y}=\frac16\end{cases}\Rightarrow\begin{cases}\frac{4}{y}=\frac12\\ \frac{1}{x}=\frac16-\frac{1}{y}\end{cases}\)
=>\(\begin{cases}y=8\\ \frac{1}{x}=\frac16-\frac18=\frac{1}{24}\end{cases}\Rightarrow\begin{cases}y=8\\ x=24\end{cases}\) (nhận)
Vậy: thời gian làm riêng của người thứ nhất và người thứ hai lần lượt là 24(ngày) và 8(ngày)
Bài 3:
Gọi số sản phẩm tổ 1 và tổ 2 làm được trong tháng thứ nhất lần lượt là x(sản phẩm) và y(sản phẩm)
(Điều kiện: x,y∈N*)
Tổng số sản phẩm hai tổ làm được trong tháng thứ nhất là 500 sản phẩm nên x+y=500(3)
Số sản phẩm tổ 1 làm được trong tháng thứ hai là: \(x\left(1+10\%\right)=1,1x\) (sản phẩm)
Số sản phẩm tổ 2 làm được trong tháng thứ hai là:
\(y\left(1+15\%\right)=1,15y\) (sản phẩm)
Tổng số sản phẩm hai tổ làm được trong tháng thứ hai là 564 sản phẩm nên 1,1x+1,15y=564(4)
Từ (3),(4) ta có hệ phương trình:
\(\begin{cases}x+y=500\\ 1,1x+1,15y=564\end{cases}\Rightarrow\begin{cases}1,1x+1,1y=550\\ 1,1x+1,15y=564\end{cases}\)
=>\(\begin{cases}1,1x+1,15y-1,1x-1,1y=564-550=14\\ x+y=500\end{cases}\)
=>\(\begin{cases}0,05y=14\\ x+y=500\end{cases}\Rightarrow\begin{cases}y=280\\ x=500-280=220\end{cases}\) (nhận)
Vậy: số sản phẩm tổ 1 và tổ 2 làm được trong tháng thứ nhất lần lượt là 220(sản phẩm) và 280(sản phẩm)

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: ab=40 và (a+3)(b+3)=ab+48
=>a+b=16 và ab=40
=>a=8+2căn 6
=>b=8-2 căn 6
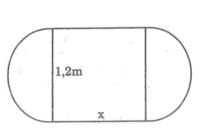
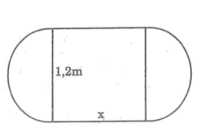
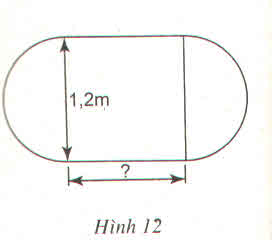



Chu vi mặt bàn sau khi nới rộng là : π.1,2 + 2x (m)
Theo đề bài,chu vi của bàn tăng gấp đôi sau khi nới rộng. Ta có:
1,2π + 2.x = 2.1,2π
⇔ 2x =2,4π -1,2π = 1,2π
⇔
Vậy kích thước còn lại của hình chữ nhật phải là 1,884m