Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

> O x M 7 -7 π/3
Quỹ đạo chuyển động là 14 cm → A = 7 cm.
Tại thời điểm ${t_0}$ chất điểm ở vị trí M có pha ban đầu là –π/3; độ lớn gia tốc cực đại tại biên.
→ từ M đến biên lần thứ 3 thì ∆φ = π/3 + 2π = 7π/3 rad.
→ t = ∆φ/ω = 7/6 s và s = 3,5 + 28 = 31,5 cm
→ v = s/t = 27 cm/s.

Trong dao động cưỡng bức, biên độ đạt cực đại khi hiện tượng cộng hưởng xảy ra.
Suy ra \(1,25 < f_0 < 1,3\)
→ \(2,5\pi < \omega < 2,6\pi\)
Có \(k = m \omega ^2\) → \(13,3 < k < 14,4\)
→ \(k \approx 13,64 N/m\).

1,vật qua vị trí x=-5 => thay x vào phương trình dao động .
2,T=0,4 s=> t=1s=2,5 T=2T+0,5T. 2chu kì sẽ đi qua x=1 bốn lần,thêm một nửa chu kì nữa được 1 lần.tổng cộng là 5 lần. Vẽ đường tròn ra nha cậu
3, denta t= 4,625-1=3,625 s=3,625 T=3T+1/2 T+1/8 T
tại t1=1s,x=căn 2.
quãng đường đi được trong 3,625 T=3. 4A+2A+A căn 2/2 .Vì một ch kì vật đi được 4A,cậu cũng vè đường tròn ra là thấy
S=29,414 cm ,v=S/t= 29,414/3,625=8,11 cm/s.
4.Tự làm nốt nhé,cứ ốp vào dường tròn là ra ngay.

Câu 1:
M A B 11 14 20
a) Bước sóng \(\lambda = 6cm\)
PT sóng do A truyền đến M: \(u_{AM}=5\cos(20\pi t-\dfrac{2\pi.11}{6})=5\cos(20\pi t-\dfrac{11\pi}{3})\)
PT sóng do B truyền đến M: \(u_{BM}=5\cos(20\pi t+\pi-\dfrac{2\pi.14}{6})=5\cos(20\pi t+\pi-\dfrac{2\pi.14}{6})=5\cos(20\pi t-\dfrac{11\pi}{3})\)
PT sóng tổng hợp tại M: \(u_M=u_{AM}+u_{BM}=10\cos(20\pi t-\dfrac{11\pi}{3})\)
b)
A B D C 20 15 P 25
Số điểm dao động cực đại trên đoạn AB: \(2.[\dfrac{AB}{\lambda}+0,5]=2.[\dfrac{20}{6}+0,5]=8\)
Điểm P trên đoạn AC dao động cực đại khi: \(PB-PA=k.\lambda =6.k\)
Suy ra: \((0-20)<6k<(25-15)\Rightarrow -3,33< k <1,67\)
\(\Rightarrow k = -3,-2,-1,0,1\)
Vậy có 5 điểm dao động cực đại
c) Bạn viết PT điểm M1, M2 (tương tự như câu a), suy ra pt vận tốc của 2 điểm, rồi lập tỉ số vận tốc là ra thôi (hai điểm này chỉ hoặc là cùng pha, hoặc là ngược pha)

Độ lệch pha giữa hai dao động là ∆φ = 0,75π – 0,5π = 0,25π rad.

Ta có: \(\dfrac{\pi x}{4}=\dfrac{2\pi x}{\lambda}\Rightarrow \lambda = 8cm\)
Chu kì: \(T=1s\)
Tốc độ truyền sóng: \(v=\dfrac{\lambda}{T}=8cm/s\)

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Tần số góc trong dao động điều hoà của con lắc lò xo là: \(\omega=\sqrt{\dfrac{k}{m}}\)

1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)
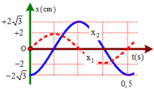


Đáp án C
Dễ thấy rằng hai dao động vuông pha nhau
=>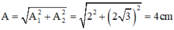
Mặc khác chu kì của dao động là T = 0,5 s => ω = 4 π rad/s.
→ Tốc độ dao động cực đại của vật