Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án A
Phương pháp: Sử dụng phương trình li độ và gia tốc của dao động điều hòa, kết hợp kĩ năng đọc đồ thị.
Cách giải:
+ Phương trình của li độ và gia tốc: 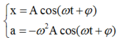
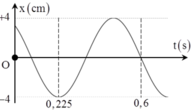
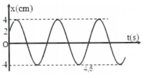
+ Từ đồ thị ta thấy: T/2 = 8 ô, 1 ô = 0,1s T = 1,6s 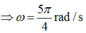
+ Tại t = 0,3s có x = 0 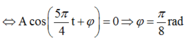
+ Tại t = 0,3s có x = 2cm 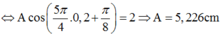
=> Phương trình của gia tốc: 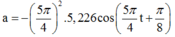
+ Tại t = 0,9s 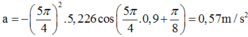

Chọn đáp án B
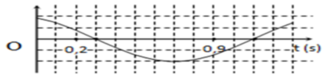
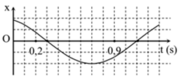
Dựa vào đồ thị ta có:
T = 1 , 6 s ⇒ ω = 5 π 4 r a d / s ;
x = A cos 5 π 4 . t + π 8 c m
Tại thời điểm t = 0,2 s, chất điểm có li độ 2 cm suy ra:
2 = A cos 5 π 4 .0 , 2 + π 8 c m ⇒ A ≈ 5 , 2 c m
a = − ω 2 A . cos 5 π 4 . t + π 8
= − 5 π 4 2 .5 , 2. cos 5 π 4 .0 , 9 + π 8
= 57 c m / s 2

Đáp án B
Từ đồ thị ta có: T 2 = 1,1 – 0,3 = 0,8 (s) ð T = 1,6 s
ð w = 2 π t = 2 π 1 , 6 = 1,25π (rad/s); thời điểm t = 0,7 s thì
x = -A=Acos(1,25π.0,7 + j) ð cos(1,25π.0,7 + j) = - 1 = cosπ
ð j = π – 0,785π = π 8 ; thời điểm t = 0,2 s thì x = 2 = Acos(1,25π.0,2 + π 8 )
ð A = 5,226 (cm); thời điểm t = 0,9 s thì
a = - w2x = - (1,25π)2.5,226.cos(1,25π.0,9 + π 8 ) = 56,98679 (cm/s2).

Đáp án C
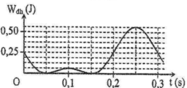
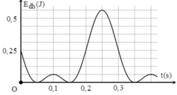
Con lắc dao động điều hòa theo phương thẳng đứng
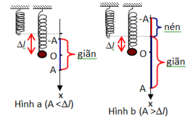
Từ đồ thị => gốc thế năng đàn hồi ở vị trí lò xo có độ dài tự nhiên và thuộc trường hợp A>Δl
Từ đồ thị ta có mỗi dòng ngang có mức thế năng: 0,25 /4 = 0,0625J.
Ta có, thế năng đàn hồi của lò xo: W t = 1 2 k x 2 (x là độ biến dạng của lò xo so với vị trí lò xo có độ dài tự nhiên). Từ đồ thị ta thấy:
+ Tại vị trí lò xo không biến dạng: Wt = 0
+ Tại vị trí vật lên cao nhất: x= A-Δl -> thế năng đàn hồi:
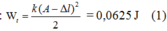
+ Tại vị trí vật xuống thấp nhất:x= A+Δl -> thế năng đàn hồi cực đại :
![]()
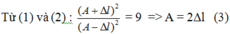
+ Chu kì dao động của con lắc:T= 0,3s
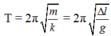
![]()
Suy ra A =2Dl0 = 4,5cm. Từ k ( A - ∆ l ) 2 2 = 0 , 0625
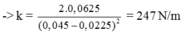
Từ T = 2 π m k
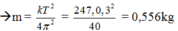

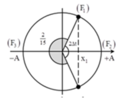
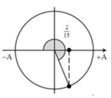
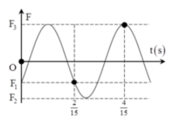
Lực đàn hồi của lò xo được xác định bằng biểu thức F = - k ( ∆ l 0 + x ) với ∆ l 0 là độ biến dạng của lò xo tại vị trí cân bằng và x là li độ của vật.
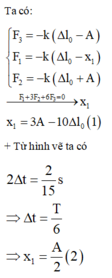
Từ (1) và (2) ta tìm được
∆ l 0 = 0 , 25 A
+ Tỉ số giữa thời gian lò xo giãn và nén trong một chu kì là
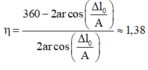
Đáp án B