Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Áp dụng định luật bảo toàn động lượng
Cách giải:
Gọi vận tốc của hệ ngay sau khi va chạm là v. Áp dụng định luật bảo toàn động lượng ta có:

Đáp án A

Đáp án C
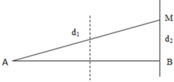
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2


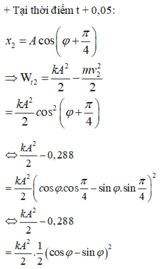


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Tốc độ trung bình = quãng đường / thời gian.
Quãng đường: \(S=A+\dfrac{A}{2}=\dfrac{3A}{2}\)
Biểu diễn dao động bằng véc tơ quay, véc tơ quay được góc là: 90 + 30 = 1200.
Thời gian tương ứng: \(t=\dfrac{120}{360}T=\dfrac{T}{3}\)
Tốc độ trung bình: \(v_{TB}=\dfrac{S}{t}=\dfrac{9A}{2T}=\dfrac{9A.\omega}{2.2\pi}=\dfrac{9v_{max}}{4\pi}\)

Gia tốc tỉ lệ với li độ, nên li độ tại B gấp đôi li độ tại A.
Giả sử li độ của A là x, thì của B là -2x (ngược dấu)
Li độ của M là: x - (x+2x) . 2 /3 = -x
Do vậy, gia tốc tại M là 3cm/s2
P/S: Đáp án chẳng liên quan gì nhỉ :)
rad/s là đơn vị của tần số góc ω chứ.

Lời giải:
Vì tại thời điểm ban đầu vật đang qua VTCB theo chiều âm nên phương trình dao động của vật \(x=A\cos\left(\omega t+\frac{\pi}{2}\right)\) (cm)
Từ điều kiện đề bài kết hợp với công thức \(A^2=x^2+\left(\frac{v}{\omega}\right)^2\) nên \(\omega=2\pi\Rightarrow A=5\left(cm\right)\)
Do đó phương trình là \(x=5\cos\left(2\pi t+\frac{\pi}{2}\right)\left(cm\right)\)

Do \(\alpha_0=8^0\) nên đây là dao động điều hòa, ta tính toán giống như một dao động điều hòa thôi.
Tại vị trí \(W_đ=W_t\)
\(\Rightarrow W=W_đ+W_t=2W_đ\)
\(\Rightarrow v_{max}^2=2.v^2\)
\(\Rightarrow v=\dfrac{v_{max}}{\sqrt 2}=\dfrac{\omega.A}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\sqrt{\dfrac{g}{\ell}}.\alpha_0.\ell}{\sqrt 2}=\dfrac{\alpha_0.\sqrt{g.\ell}}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\dfrac{8.\pi}{180}.\sqrt{10.1}}{\sqrt 2}\approx0,31(m/s)\)
Bài này thiếu điều kiện em nhé.
Hoặc là cần có hình vẽ, hoặc là phải có thời điểm ban đầu chất điểm đang ở đâu.
Về liên hệ giữa chuyển động tròn đều với dao động của hình chiếu chất điểm lên 1 trục nằm ngang thầy có một bài viết ở đây, em tham khảo:
Các kiến thức bổ trợ chương trình vật lý 12 | Học trực tuyến
Ui ko nhớ là từng trả lời câu hỏi này lun ớ, để trả lời lại < Em tính ra kết ủa mà sao thầy phynit kêu ko được nhỉ '-' >
Ok let's start
\(T=\pi\left(s\right)\Rightarrow\omega=\frac{2\pi}{T}=2\left(rad/s\right)\)
Áp dụng công thức ko thời gian:
\(A^2=x^2+\frac{v^2}{\omega^2}\Rightarrow R^2=2^2+\frac{4^2}{2^2}\Rightarrow R=A=2\sqrt{2}\left(cm\right)\)
\(x=A\cos\left(\omega t+\varphi\right)\Rightarrow\cos\left(\omega t+\varphi\right)=\frac{2}{2\sqrt{2}}=\cos\frac{\pi}{4}\)
\(\Rightarrow\phi=\omega t+\varphi=\pm\frac{\pi}{4}\)
\(v=4\left(cm/s\right)>0\Rightarrow\) vật đi theo chiều dương \(\Rightarrow\phi< 0\Rightarrow\phi=-\frac{\pi}{4}\left(rad\right)\)