Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

30'=0,5h
a) Tốc độ người đó trên doạn đường AB là:
vAB= \(\frac{s_{AB}}{t_1}=\frac{4,5}{0,5}=9\)(km/h)
b) Độ dài BC là:
sBC=v2.t2= 5.0,4 = 2(km)
c) gọi tolà thời gian nghỉ
12'=0,2h
Vận tốc trung bình trên cả đoạn AD là
vtb= \(\frac{s_{AB}+s_{AC}+s_{CD}}{t_1+t_2+t_3+t_o}=\frac{4,5+2+3}{0,5+0,4+0,5+0,2}=5,9375\)(km/h)

mÌNH MỎI TAY QUÁ
Lấy gốc tọa độ tại AA chiều dương là chiều từ AA đến BB. Gốc thời gian là lúc 7h7h
Phương trình chuyển động của :
Xe đi từ A:A: xA=36t(km−h)xA=36t(km−h)
Xe đi từ B:xB=96−28t(km−h)B:xB=96−28t(km−h)
Hai xe gặp nhau khi :xA=xB:xA=xB
→36t=96−28t→36t=96−28t
⇒t=1,5(h)⇒t=1,5(h)
xA=36t=36.1,5=54(km)xA=36t=36.1,5=54(km)
Hai xe gặp nhau lúc 8h30′8h30′. Nơi gặp nhau cách AA 54km54km
TH1:TH1: Hai xe cách nhau 24km24km trước khi hai xe gặp nhau
Hai xe cách nhau 24km
⇔⇔ xB−xA=24xB−xA=24
⇔⇔ 96−28t′−36t′=2496−28t′−36t′=24
⇔t′=1,125h⇔t′=1,125h
Vậy lúc 8h7phút30giây hai xe cách nhau 24km
TH2:TH2: Hai xe cách nhau 24k sau khi gặp nhau
Hai xe cách nhau 24km
⇔xA−xB=24⇔xA−xB=24
⇔36t′′−96+28t′′=24⇔36t″−96+28t″=24
⇔t′′=1,875(h)⇔t″=1,875(h)
Vậy lúc 8h52phút30giây hai xe cách nhau 24km
bài 2:
ta có:
thời gian người đó đi trên nửa quãng đường đầu là:
t1=S1/v1=S/2v1=S/24
thời gian người đó đi hết nửa đoạn quãng đường cuối là:
t2=S2/v2=S2/v2=S/40
vận tốc trung bình của người đó là:
vtb=S/t1+t2=S/(S/40+S/24)=S/S(140+124)=1/(1/24+1/40)
⇒vtb=15⇒vtb=15 km/h
bài 3:
thời gian đi nửa quãng đầu t1=(1/2) S.1/25=S/50
nửa quãng sau (1/2) t2.18+(1/2) t2.12=(1/2) S⇔t2=S/30
vận tốc trung bình vtb=S/(t1+t2)=S/S.(1/50+1/30)=1/(1/50+1/30)=18,75(km/h)
HT

a) Chất điểm X và Y gặp nhau tại E ( khi X vừa rời đi khỏi E thì gặp Y chạy ngược chiều )
Khi chất điểm X đến C thì chất điểm Y cũng chuyển động từ E đến A rồi quay lại C gặp chất điểm X tức là thời gian đi của chúng là như nhau = 8s
Ta có Quãng đường chất điểm Y đi từ E lần lượt là: EA=20(m) rồi tiếp tục quay ngược đi thêm đoạn EA=20(m) và đoạn EC=v1.t=32(m) từ đây suy ra thời gian đi của chất điểm Y là: \(\dfrac{20}{v_y}+\dfrac{20}{v_y}+\dfrac{32}{v_y}\)
Theo điều ta vừa lập luận ở trên 2 chất điểm X và Y có thời gian đi như nhau nên ta có:
\(\dfrac{20}{v_y}+\dfrac{20}{v_y}+\dfrac{32}{v_y}=8\) Từ đây \(\Rightarrow v_y=\dfrac{20+20+32}{8}=9\left(m/s\right)\)

thời điểm gặp nhau cách thời điểm xuất phát là: \(75\dfrac{9}{70}\left(phút\right)\)
vị trí gặp nhau cách A: \(\approx33,9km\)

Bài giải :
Thời gian xe đi hết \(\dfrac{1}{3}\) quãng đường đầu là :
\(t_1=\dfrac{\dfrac{s}{3}}{50}=\dfrac{s}{150}\left(h\right)\)
Thời gian xe đi hết \(\dfrac{2}{3}\) quãng đường còn lại là :
\(t_2=\dfrac{2s}{3}:v_2=\dfrac{2s}{3v_2}\left(h\right)\)
Trong 2/3 thời gian xe chạy được quãng đường là :
\(s_1=\dfrac{2}{3}t.60=40t\) (km)
1/3 thời gian xe chạy đc quãng đường là :
\(s_2=\dfrac{1}{3}t.60=20t\left(km\right)\)
Ta có : \(\dfrac{s}{2}=s_1+s_2=40t+20t=60t\)
=> \(t=\dfrac{s}{120}\left(h\right)\)
Vận tốc trung bình của xe trên cả đoạn đường AB là :
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{s}{\left(t_1+t_2+t\right)}=\dfrac{s}{\dfrac{s}{150}+\dfrac{2s}{3v_2}+\dfrac{s}{120}}=\dfrac{1}{\dfrac{1}{150}+\dfrac{2}{3v_2}+\dfrac{1}{120}}\)
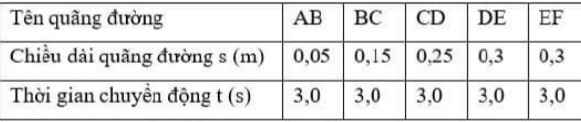 Hãy tính tốc độ trung bình của chất điểm khi nó chuyển động trên:
Hãy tính tốc độ trung bình của chất điểm khi nó chuyển động trên:
a)\(v_{tb}=\dfrac{s_{AB}+s_{BC}}{t_{AB}+t_{BC}}=\dfrac{0,05+0,15}{3+3}=0,03\left(m/s\right)\)
b)\(v_{tb}=\dfrac{0,05+0,15+0,25}{3+3+3}=0,05\left(m/s\right)\)
c)\(v_{tb}=\dfrac{0,05+0,15+0,25+0,3}{3+3+3+3}=0,0625\left(m/s\right)\)
d)\(v_{tb}=\dfrac{0,05+0,15+0,25+0,3+0,3}{3+3+3+3+3}=0,07\left(m/s\right)\)