Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ minh họa.
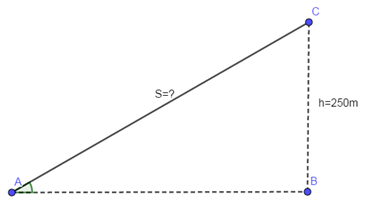
Độ dài đoạn AC chính là quãng đường máy bay cần đi để đạt độ cao 250m.
Xét tam giác ABC vuông tại B có:
sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)
Vậy máy bay cần bay quãng đường 640 (m) để đạt được độ cao 250 (m).

trả lời
e chưa học đến
chị lên học 24 hỏi nha
chúc chị học tốt
Bài 1 :
A B E C
Tính được CE = 2tan300 \((m)\)
Suy ra BC = 2CE = 4 tan 30 \(\approx2,3m\)
Vậy các bạn phải cắm cọc cố định cách nhau 2,3m
Bài 2 : Tham khảo : https://vndoc.com/de-thi-tham-khao-vao-lop-10-mon-toan-truong-thcs-doan-ket-quan-6-nam-hoc-2019-2020/download

Chiều cao của cây:
\(h=20.tan30^0\approx12\left(m\right)\)

Độ cao của máy bay là cạnh góc vuông đối diện với góc 3 ° , khoảng cách từ máy bay đến sân bay là cạnh huyền
Vậy khoảng cách từ máy bay đến sân bay là:


Diều bay cao \(\sin70^0\cdot20\approx19\left(m\right)\)

Chiều cao của tháp là: \(24.tan32^0\approx15\left(m\right)\)

Lời giải:
Đoạn đường máy bay phải đi là:
$2500:\sin 23^0=6398$ (mét)