Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)

Chiều cao tháp:
\(h=400.tan39^0+1,1\approx325\left(m\right)\)

Ta có :
∠ABC=90°−60°=30°,∠ACB=90°+30°=120°⇒∠CAB=180°−30°−120°=30°⇒∠ABC=∠CAB∠���=90°−60°=30°,∠���=90°+30°=120°⇒∠���=180°−30°−120°=30°⇒∠���=∠���
⇒ΔCAB⇒���� cân tại C⇒AC=BC=100m⇒��=��=100�
Ta có:h=AC.sin30°=100.12=50m

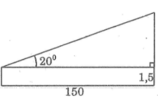
Phần còn lại của cột ăng-ten là cạnh đối của góc 20 ° , khoảng cách từ chỗ em đứng đến chân cột ăng-ten là cạnh kề với góc 20 °
Phần còn lại của cột ăng-ten cao là:
150.tg 20 ° ≈ 54,596 (m)
Chiều cao của cột ăng-ten là:
54,596 + 1,5 = 56,096 (m)
Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)