Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(x\left(km/h\right)\) là vận tốc thực của ca nô. \(\left(x>4\right)\)
Vì vận tốc dòng nước là \(4km/h\) nên vận tốc của ca nô lúc xuôi dòng là \(x+4\left(km/h\right)\) và vận tốc lúc ngược dòng là \(x-4\left(km/h\right)\)
Vì quãng sông AB dài 24km nên thời gian ca nô xuôi dòng từ A đến B là \(\dfrac{24}{x+4}\left(h\right)\), thời gian ca nô ngược dòng từ B về A là \(\dfrac{24}{x-4}\left(h\right)\)
Mà tổng thời gian ca nô xuôi và ngược dòng là \(3h12p=\dfrac{16}{5}h\) nên ta có pt \(\dfrac{24}{x+4}+\dfrac{24}{x-4}=\dfrac{16}{5}\)\(\Leftrightarrow\dfrac{1}{x+4}+\dfrac{1}{x-4}=\dfrac{2}{15}\)\(\Leftrightarrow\dfrac{\left(x-4\right)+\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{2}{15}\)\(\Leftrightarrow\dfrac{2x}{x^2-16}=\dfrac{2}{15}\)\(\Leftrightarrow\dfrac{x}{x^2-16}=\dfrac{1}{15}\)\(\Rightarrow x^2-16=15x\)\(\Leftrightarrow x^2-15x-16=0\) (1)
pt (1) có \(a-b+c=1-\left(-15\right)-16=0\) nên pt này có 2 nghiệm:
\(x_1=-1\) (loại) và \(x_2=-\dfrac{-16}{1}=16\) (nhận)
Vậy vận tốc thực của ca nô là \(16km/h\)

Đáp án A
Đổi 7 giờ 30 phút= 15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h; x > 3).
vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là: 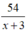 (h)
(h)
Thời gian của ca nô khi ngược dòng sông từ B về A là: 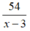 (h)
(h)
Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
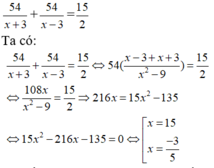
Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.
Vậy vận tốc thực của ca nô là 15 (km/h).

Đổi 8 giờ 6 phút = 81/10 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 2
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 2 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 72/(x+2) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 72/(x-2) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 8 giờ 6 phút nên ta có phương trình:
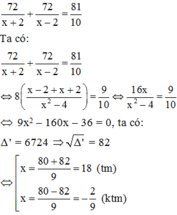
Vậy vận tốc thực của ca nô là 18 (km/h)
Đáp án: A

Đổi 7 giờ 30 phút =15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h), x > 3
Vận tốc của ca nô khi xuôi dòng sông từ A đến B là x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là 54/(x+3) (h)
Thời gian của ca nô khi ngược dòng song từ B về A là 54/(x-3) (h)
Do ca nô chạy xuôi dòng từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
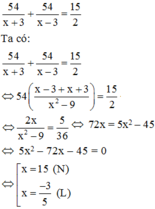
Vậy vận tốc thực của ca nô là 15 (km/h)
Đáp án: D

gọi vận tốc thực là x(x>4)km/h
vận tốc khi xuôi dòng là x+4 km/h
vận tốc khi ngược dòng là x-4 km/h
thời gian ca nô đi xuôi dòng là \(\dfrac{80}{x+4} \)h
thời gian ca nô đi ngược dòng là \(\dfrac{80}{x-4} \)h
vì tổng thời gian ca nô đi xuôi dòng và ngược dòng là 8h20p=\(\dfrac{25}{3} \)h
nên ta có pt \(\dfrac{80}{x+4} \)+\(\dfrac{80}{x-4} \)=\(\dfrac{25}{3} \)
giải pt x=-0.8 Ktm điều kiện
x= 20 TM
vậy vận tốc thực của ca nô là 20km/h

Gọi vận tốc của ca nô khi nước yên lặng là x ( km/h ; x > 4 )
=> Vận tốc ca nô khi xuôi dòng = x + 4 ( km/h )
=> Thời gian ca nô đi xuôi dòng = 30/(x+4) ( giờ )
=> Vận tốc ca nô khi ngược dòng = x - 4 ( km/h )
=> Thời gian ca nô đi ngược dòng = 30/(x-4) ( giờ )
Tổng thời gian xuôi và ngược dòng = 4 giờ
=> Ta có phương trình \(\frac{30}{x+4}+\frac{30}{x-4}=4\)
<=> \(\frac{30x-120}{\left(x-4\right)\left(x+4\right)}+\frac{30x+120}{\left(x-4\right)\left(x+4\right)}=\frac{4x^2-64}{\left(x-4\right)\left(x+4\right)}\)
=> 60x = 4x2 - 64
<=> x2 - 14x - 15 = 0
<=> ( x + 1 )( x - 15 ) = 0
<=> x = -1 ( ktm ) hoặc x = 15 ( tm )
Vậy ...
gọi x (km/h) là vận tốc của ca nô khi dòng nước đứng yên (đk x lớn hơn 2)
vận tốc xuôi dòng của ca nô là: x+4
vận tốc ngược dòng của ca nô là:x -4
thời gian xuôi dòng của ca nô là :30\x+4
thời gian ngược dòng của ca nô là :30/x-4
theo bài ra ta có pt:30/x+4 +30/x-4 =4