Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi F h là lực hãm. Muốn thang xuống đều thì ta phải có:
T ' + F h = P → F h = P − T ' = 6000 − 5400 = 600 N .
Công của lực hãm là: A h = F h . s = 600 . 150 = 90 . 000 J = 90 k J .
Chọn đáp án A

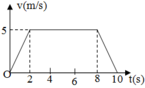
Gia tốc của vật trong từng giai đoạn chuyển động
+ GĐ 1: a 1 = v 2 − v 1 t 1 = 5 − 0 2 = 2 , 5 m / s 2
+ GĐ 2: a 2 = v 3 − v 2 t 2 = 5 − 5 8 = 0 m / s 2
+ GĐ 3: a 3 = v 2 − v 2 t 3 = 0 − 5 2 = − 2 , 5 m / s 2
a. + Giai đoạn 1: Thang máy đi lên nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
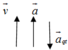
⇒ g / = 10 + 2 , 5 = 12 , 5 m / s 2 ⇒ T = P / = m g / = 1000.12 , 5 = 12500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2
⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi lên chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t

⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
b. Thang máy đi xuống
+ Giai đoạn 1: Đi xuống nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t
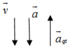
⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2 ⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi xuống chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t

a) Khi thang máy đứng yên, lực kế chỉ trọng lượng thật của người:
![]()
b) Khi thang máy đi xuống nhanh dần đều:
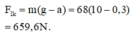
c) Khi thang máy đi xuống chậm dần đều:
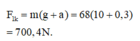

a. Muốn kéo thang máy lên thì lực căng cực tiểu T phải bằng trọng lượng P của thang: T = P = mg = 600.10 = 6000N.
Công cực tiểu của lực căng T là:Amin = T.s = 900000J = 900kJ
b, Gọi Fh là lực hãm. Muốn thang xuống đều thì ta phải có:
T’ + Fh = P Fh = P – T’= 6000 – 5400 = 600N.
Công của lực hãm là: Ah = Fh.s = 600.150 = 90.000J = 90kJ.

a) Khi thang máy đi lên đều, lực kéo của động cơ chính bằng trọng lượng của thang máy: F = P
Công của động cơ để kéo thang máy khi đi lên đều:
A = m.g.h = 800.10.10 = 80000J
b) Khi thang máy đi lên nhanh dần đều, theo định luật II – Niu tơn:
\(\overrightarrow{F}+\overrightarrow{P}=m.\overrightarrow{a}\)
Chiếu theo phương chuyển động:
F − P = ma => F = P + ma = m.(g + a)
=> F = 800.(10+1) = 8800N
Công của động cơ để kéo thang máy khi đi lên nhanh dần:
A = F.s = 8800.10 = 88000Jbạn giải dùm mình câu dưới nữa đi câu 1 vật có khối lượng 2kg đó

a, Ngoại lực tác dụng lên thang máy là trọng lực và kéo của động cơ thang máy. Áp dụng định lý về động năng ta có: Wđ1 – Wđ0 = A F 1 → + A P 1 →
Mà Wđ1 = m . v 1 2 2 , Wđ0 = m . v 0 2 2 = 0 ;
A P 1 → = − P . s 1 = − m . g . s 1 ( A P → 1 < 0 )
Vì thang máy đi lên
⇒ A F 1 = m . v 1 2 2 + m . g . s 1 = 1 2 .1000.5 2 + 1000.10.5 = 62500 J
b, Vì thang máy chuyển động đều, lực kéo của động cơ cân bằng với trọng lực P → : F 2 → + P → = 0 . Công phát động của động cơ có độ lớn bằng công cản A F 2 → = − A P → với A P = − P . s 2 = − m . g . s 2
=> AF2 = mgs2 do đó công suất của động cơ thang máy trên đoạn đường s2 là:
℘ 2 = A F 2 t = m . g . s 2 t = m . g . v 2 = m . g . v 1 ⇒ ℘ 2 = 1000.10.5 = 50000 ( W ) = 50 ( k W ) .
c, Ngoại lực tác dụng lên thang máy là trọng lực P → và lực kéo F 3 → của động cơ.
Áp dụng định lí động năng ta có: Wđ3 – Wđ2 = AF3 + Ap’
Mà Wđ3 = m . v 3 2 2 = 0 ; Wđ2 = m v 2 2 2 (v2 = v1 = 5m/s); Ap = - Ps3 = - mgs3
Công của động cơ trên đoạn đường s3 là: AF3 = mgs3 - m v 2 2 2 = 37500J
Áp dụng công thức tính công ta tìm được lực trung bình do động cơ tác dụng lên thang máy trên đoạn đường s3: F 3 ¯ = A F 3 s 3 = 37500 5 = 7500 N

\(a=\dfrac{v}{t}=\dfrac{2}{4}=0,5m/s^2\)
\(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,5.4^2=4m\)
\(F-P=ma\Rightarrow F=P+ma=m\left(g+a\right)=800.\left(10+0,5\right)=8400N\)
\(P=\dfrac{Fs}{t}=\dfrac{8400.4}{4}=8400W\)

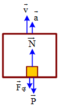
Chọn Oy thẳng đứng chiều + hướng lên
v v F P k > > v v O y
Ta có: \(\overrightarrow{F_k}+\overrightarrow{P}=m\overrightarrow{a}\)
=> Fk - P = ma
=> 12000- mg =ma
<=> 12000- 1000.10=1000.a
=> a = 2m/s2
\(s=v_0t+\frac{1}{2}at^2=0+\frac{1}{2}.2.t^2\)
<=> \(t=5\left(s\right)\)
\(v=v_0+at=2.5=10\left(m/s\right)\)
b) \(a=\frac{0-10^2}{2.20}=-2,5\left(m/s^2\right)\)
\(\text{=> Fk = P +F = mg +ma = m(g+a) = 1000.(10-2,5) =7500(N)}\)