Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử bộ nguồn này có m dãy, mỗi dãy gồm n nguồn mắc nối tiếp, do đó nm = 20. Suất điện động và điện trở trong của bộ nguồn này là :
E b = n E 0 = 2n;
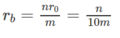
Áp dụng định luật Ôm cho toàn mạch ta tìm được cường độ dòng điện chạy qua điện trở R là :
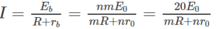
Để I cực đại thì mẫu số của vể phải của (1) phải cực tiểu. Áp dụng bất đẳng thức Cô-si thì mẫu số này cực tiểu khi : mR = n 0 . Thay các giá trị bằng số ta được : n = 20 và m = 1.
Vậy để cho dòng điện chạy qua điện trở R cực đại thì bộ nguồn gồm m = 1 dãy với n = 20 nguồn đã cho mắc nối tiếp.

đáp án B
ξ b = m ξ = 2 m r b = m r n = 0 , 1 m n = m 2 120 ⇒ I = ξ b R + r b = 2 m R + m 2 120 = 240 m + 120 m ≤ 120 R
⇒ I max = 120 R ⇔ m = 120 R = 6 ⇒ n = 2

Mắc hai nguồn nối tiếp:
\(\xi_b=n\cdot\xi=2\xi\)
\(r_b=n\cdot r=2r\)
\(\Rightarrow I_1=\dfrac{\xi_{b1}}{r_{b1}}=\dfrac{2\xi}{2r}=\dfrac{\xi}{r}\)
Mắc song song:
\(\xi_b=\xi\)
\(r_b=\dfrac{r}{n}=\dfrac{r}{2}\)
\(\Rightarrow I_2=\dfrac{\xi_{b2}}{r_{b2}}=\dfrac{\xi}{\dfrac{r}{2}}=2\cdot\dfrac{\xi}{r}=2I_1\)
\(\Rightarrow\dfrac{I_1}{I_2}=\dfrac{1}{2}\)
Mắc hai nguồn nối tiếp:
\(\xi_b=n\cdot\xi=2\xi\)
\(r_b=n\cdot r=2r\)
\(\Rightarrow I_1=\dfrac{\xi_b}{r_{b1}+r}=\dfrac{2\xi}{3r}\)
Mắc hai nguồn song song:
\(\xi_b=\xi\)
\(r_b=\dfrac{r}{n}=\dfrac{r}{2}\)
\(\Rightarrow I_2=\dfrac{\xi_{b2}}{r_{b2}+r}=\dfrac{\xi}{\dfrac{r}{2}+r}=\dfrac{\xi}{\dfrac{3}{2}r}=\dfrac{2}{3}\cdot\dfrac{\xi}{r}\)
Vậy \(\dfrac{I_1}{I_2}=1\)
Chọn C

Đáp án B
I = E R + r = E 2 R I ' = 3 E R + 3 r = 3 E 4 R ⇔ I ' I = 3 2 ⇔ I ' = 1 , 5 I
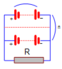
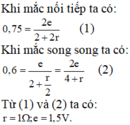
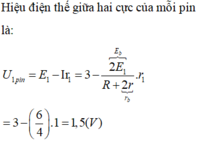

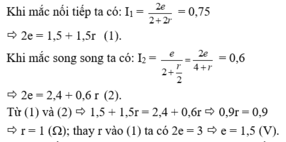

Cái gì thế này?
Suất điện động của bộ nguồn là: \(ξ_b=5.ξ=5.1,2=6V \)
Điện trở trong của bộ nguồn là: \(r_b=5.r\)
Có: \(H=\frac{R_N}{R_N+r_b}.100\Rightarrow80=\frac{2}{2+5.r}.100\Rightarrow r=0,1\Omega\)
Cường độ dòng điện chạy qua mạch điện là: \(I=\frac{\text{ξ}_b}{R_N+r_b}=\frac{6}{2+0,1.5}=2,4A\)