Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(m_1;m_2\) là khối lượng khí trong bình trước và sau khi đun nóng bình. Áp dụng phương trình Menđêlêep - Clapêrông ta có: \(pV=\frac{m_1}{\mu}RT_1;pV=\frac{m_2}{\mu}RT_2\)
Từ đó suy ra khối lượng khí đã thoát ra:
\(m_2-m_1=\frac{pV\mu}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\), với \(p=50atm,V=10\)lít \(,\mu=2g\)
\(R=0,084atm.l\text{/}mol.K;\)\(T_1=7+273=280K\)
\(T_2=17+273=290K\). Suy ra \(m_2-m_1=1,47g\)
Gọi m1,m2m1,m2 là khối lượng khí trong bình trước và sau khi đun nóng bình. Áp dụng phương trình Menđêlêep - Clapêrông ta có: pV=m1μRT1,pV=m2μRT2pV=m1μRT1,pV=m2μRT2
Từ đó suy ra khối lượng khí đã thoát ra:
m2−m1=pVμR(1T1−1T2)m2−m1=pVμR(1T1−1T2), với p=50atm,V=10lít,μ=2gp=50atm,V=10lít,μ=2g
R=0,084atm.l/mol.K;T1=7+273=280KR=0,084atm.l/mol.K;T1=7+273=280K
T2=17+273=290KT2=17+273=290K. Suy ra m2−m1=1,47g

Đáp án D.
Ta có: p 1 T 1 = p 2 T 2 ⇒ T 2 = p 2 p 1 . T 1 = 1500 K = 1227 0 C

Trạng thái 1: \(\left\{{}\begin{matrix}p_1=2\cdot10^5Pa\\T_1=27^oC=300K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=???\\T_2=627^oC=900K\end{matrix}\right.\)
Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{2\cdot10^5}{300}=\dfrac{p_2}{900}\)
\(\Rightarrow p_2=6\cdot10^5Pa\)

- Chỉ ra đây là quá trình đẳng tích
- Áp dụng định luật Sác – lơ:
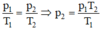
Thay số được p 2 = 4atm.

Ta có : T1 = toC + 273 = 30 + 273 = 303oK
p1 = 2 bar = 2 . 105 Pa
p2 = 4 bar = 4 . 105
Vì quá trình là đẳng tích , áp dụng định luật Charles ta có
\(\frac{p_1}{p_2}=\frac{T_1}{T_2}\)→ T2 = \(\frac{p_2.T_1}{p_1}=\frac{4.10^5.303}{2.10^5}\)= 606oK
Vậy để áp suất tăng lên gấp đôi , ta phải tăng nhiệt độ lên 606oK
* Trạng thái 1: T1 = 273 + 30 = 303 K
p1 = 2 bar
* Trạng thái 2: T2 = ? p2 = 2p1
* Vì thể tích bình không đổi nên:
\(\frac{P1}{T1}=\frac{P2}{T2}\Rightarrow T2=\frac{P2.T1}{P1}=\frac{2P1.T1}{P1}\) = 2T1 = 606 K

Ta có : \(T_1=273+43=313^0K;T_2=273+57=330^0K\)
Theo định luật Sác lơ:
\(\frac{p_1}{T_1}=\frac{p_2}{T_2}\rightarrow p_2=\frac{T_2}{T_1}p_1=\frac{330}{313}285=330,5kPa\)
Độ tăng áp suất:
\(\Delta p=p_2-p_1=300,5-285=15,5kPa\)
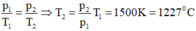
Trạng thái 1: \(\left\{{}\begin{matrix}p_1=10^5Pa\\T_1=27^oC=300K\end{matrix}\right.\)
Trạng thái 2: \(\left\{{}\begin{matrix}p_2=5\cdot10^5Pa\\T_2=???\end{matrix}\right.\)
Quá trình đẳng tích:
\(\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow\dfrac{10^5}{300}=\dfrac{5\cdot10^5}{T_2}\)
\(\Rightarrow T_2=1500K=1227^oC\)