Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có sóng dừng một đầu kín một đầu hở nên ta có
l
=
(
2
k
+
1
)
λ
4
=
(
2
k
+
1
)
v
4
f
→
v
=
4
l
f
2
k
+
1
với l=0,5 m,
300
m
/
s
≤
v
≤
350
→
k
=
2
l
=
k
λ
2
+
k
λ
4
với k=2 như vậy đổ thêm nước có hai vị trí mực nước cho âm được khuyếch đại mạnh

Các phân tử không khí trong ống dao động theo tần số của dao động của âm thoa. Sóng âm trong ống nghiệm phản xạ liên tiếp ở miệng và ở đáy ống nghiệm. Khi khoảng cách giữa hai mặt phản xạ ấy có một giá trị thích hợp thì tạo thành một hệ sóng dừng ổn định. Khi đó ở miệng ống có một bụng dao động còn ở đáy ống tức là mặt nước có một nút. Vậy độ cao h phải thoả mãn điều kiện :
h = (2k + 1) λ /4 (k = 0, 1, 2...) (1)
Thay λ = v/f vào (1), ta được h = (2k + 1) λ /4f
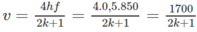
Với k = 0 ⇒ v = 1700 m/s
(loại, vì lớn hơn cỡ của tốc độ âm trong không khí)
k = 1 ⇒ v = 566,7 m/s
(loại, vì lớn hơn cỡ của tốc độ âm trong không khí)
k = 2 ⇒ v = 340 m/s
(chấp nhận vì cỡ của tốc độ âm trong không khí là 300 m/s)
k = 3 ⇒ v = 240 m/s
(loại, vì nhỏ hơn cỡ của tốc độ âm trong không khí)

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B

Đáp án A
L là chiều dài cột khí , h là chiều cao ống
Âm to nhất khi miệng ống là bụng sóng , chiều dài cột khí trong ổng thõa mãn điều kiện sau:
L = ( k + 1 2 ) λ 2
Mà 0 < L < 15cm
⇒ - 1 2 < k < 0 , 6 ⇒ k = 0
=> Nước cần đổ thêm vào để khi gõ vào âm thoa thì nghe âm phát ra to nhất là:
H = h – L = 2,5 cm.

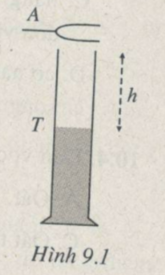
Khi đổ dần nước vào ống nghiệm đến độ cao 30cm thì thấy âm được khuyếch đại rất mạnh, có nghĩa là khi đó hiện tượng sóng dừng xảy ra, âm nghe được to nhất do tại đáy ống hình thành một nút sóng, miệng ống hình thành một bụng sóng. Mặt khác, nước cao 30cm thì cột không khí cao 50cm. Từ đó ta có:
\(300\left(\frac{1}{4.850+k\frac{1}{2.850}}\right)\le0,5=\)\(\frac{\lambda}{4}+k\frac{\lambda}{2}=v\left(\frac{1}{4f}+k\frac{1}{2f}\right)\le350\left(\frac{1}{4.850}\right)\)\(\Rightarrow1,93\le k\le2,33\Rightarrow k=2\)
\(\Rightarrow v=\frac{0,5}{\frac{1}{4.850+2.\frac{1}{2.850}}}=340\)
Từ đó dễ thấy \(\lambda\) = 40cm
Khi tiếp tục đổ nước vào ống thì chiều dài cột kí giảm dần, và để âm khuyếch đại mạnh thì chiều dài cột khí phải thỏa mãn
\(0< l=\frac{\lambda}{4}+k\frac{\lambda}{2}=10+k.20< 50\)
\(-0,5< k< 2\)
k = 0;1
Vậy khi đổ thêm nước vào thì có thêm 2 vị trí làm cho âm khuyếch đại rất mạnh
chọn A
Trước tiên ta thấy rằng trong ống lúc đổ nước và đến độ cao 30cm thì có sóng dừng giống sợi dây 1 đầu cố định, 1 đầu tự do.
Vậy ta có : \(l=\left(2k+1\right)\lambda\Rightarrow\lambda=\frac{4l}{\left(2k+1\right)}\) (2)
Mặt khác ta có: \(v=\lambda f\) (1)
Từ (1) và (2) ta có:
\(v=\frac{4lf}{2k+1}=\frac{4\left(0,8-0,3\right)850}{2k+1}=\frac{1700}{2k+1}\)
Vì vận tốc truyền âm nằm trong khoảng:
\(300\le v\le500\Rightarrow300\le\frac{1700}{2k+1}\le350\Rightarrow1,9\le k\le2,3\Rightarrow k=2\)
Vậy vận tốc truyền âm và bước sóng của âm là:
\(v=\frac{1700}{2.2+1}=340\left(\frac{m}{s}\right)\Rightarrow\lambda=\frac{v}{f}=0,4m=40cm\)
Như vậy tính cả miệng ống thì có 3 bụng sóng. Vì:
\(l=\left(2n+1\right)\frac{\lambda}{4}\Rightarrow\pi=\frac{4.50}{2.40}-0,5=2\)
N = 2+1=3 Vậy sẽ có 3 vị trí.
Vậy B đúng