
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sách hay cái zì bạn?nếu đề thi hay bài tập bạn chụp rùi gửi mail(lethihuong34567890@gmail.com) cho mk đc hơm![]() ? còn nếu sách thì chỉ cần chụp bìa dc gùi
? còn nếu sách thì chỉ cần chụp bìa dc gùi![]()

Điều kiện:
\(x-1\ne0\Rightarrow x\ne1\)
\(x^3+x\ne0\Leftrightarrow x\ne0\)

a)x^2+5y^2+2x-4xy-10y+14
=x^2+2x-4xy+5y^2-10y+14
=x^2+2x(1-2y)+5y^2=10y+14
=x^2+2x(1-2y)+(1-2y)^2+5y^2-10xy-(1=2y)^2+14
=(x+1-2y)^2+5y^2-10y-(1-4y+4y^2)+14
=(x+1-2y)^2+5y^2-10y-1+4y-4y^2+14
=(x+1-2y)^2+y^2-6y+13
=(x+1-2y)^2+(y-3)^2+4
Vì....(đpcm)
b)5x^2+10y^2-6xy-4x-2y+3
=(x^2-6xy+9y^2)+(4x^2+1-4x)+(y^2-2y+1)+1
=(x-3y)^2+(2x-1)^2+(y-1)2+1
Vì....
(đpcm)



a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)

P = (1-2x)(x-3) = -2x^2 + 7x - 3
bấm phím trên Mt casio 570VN-plus được kq: Pmin = 25/8 = 3.125
\(P=\left(1-2x\right)\left(x-3\right)\)
\(\Leftrightarrow P=x-3-2x^2+6x\)
\(\Leftrightarrow P=-2x^2+7x-3\)
\(\Leftrightarrow P=-2x^2+7x-\dfrac{49}{8}+\dfrac{25}{8}\)
\(\Leftrightarrow P=-2\left(x^2-\dfrac{7}{2}x+\dfrac{49}{16}\right)+\dfrac{25}{8}\)
\(\Leftrightarrow P=-2\left[x^2-2.x.\dfrac{7}{4}+\left(\dfrac{7}{4}\right)^2\right]+\dfrac{25}{8}\)
\(\Leftrightarrow P=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{25}{8}\)
Vậy GTLN của \(P=\dfrac{25}{8}\) khi \(x-\dfrac{7}{4}=0\Leftrightarrow x=\dfrac{7}{4}\)

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)
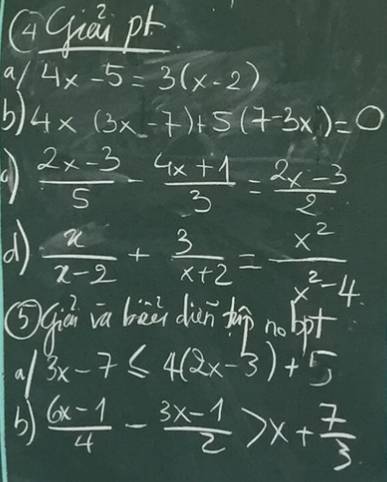

 Help me
Help me Help me
Help me
 cac
cac



4)
a)\(4x-5=3\left(x-2\right)\)
⇔\(4x-5=3x-6\)
⇔\(4x-3x=-6+5\)
⇔\(x=-1\)
Vập phương trình có nghiệm là \(x=-1\)
b)\(4x\left(3x-7\right)+5\left(7-3x\right)=0\)
⇔\(12x^2-28x+35-15x=0\)
⇔\(12x^2-48x=0\)
⇔\(12x\left(x-4\right)=0\)
⇔\(12x=0\) hoặc \(x-4=0\)
⇔\(x=0\) hoặc \(x=4\)
Vập phương trình có tập nghiệm là \(S=\left\{0;4\right\}\)
c)\(\dfrac{2x-3}{5}-\dfrac{4x+1}{3}=\dfrac{2x-3}{2}\)
⇔\(\dfrac{6\left(2x-3\right)}{5.6}-\dfrac{10\left(4x+1\right)}{3.10}=\dfrac{15.\left(2x-3\right)}{2.15}\)
⇒\(12x-18-40x-10=30x-45\)
⇔\(12x-40-30=-45+18+10\)
⇔\(-58x=-17\)
⇔\(x=\dfrac{17}{58}\)
Vập phương trình có nghiệm là \(x=\dfrac{17}{58}\)
d)\(\dfrac{x}{x-2}+\dfrac{3}{x+2}=\dfrac{x^2}{x^2-4}\)
\(ĐKXĐ:\left[{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow x\ne\mp2\)
\(\dfrac{x}{x-2}+\dfrac{3}{x+2}=\dfrac{x^2}{x^2-4}\)
⇔\(\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x^2}{\left(x+2\right)\left(x-2\right)}\)
⇒\(x^2+2x+3x-6=x^2\)
⇔\(x^2-x^2+2x+3x=6\)
⇔\(5x=6\)
⇔\(x=\dfrac{6}{5}\)
Vập phương trình có nghiệm là \(x=\dfrac{6}{5}\)
b,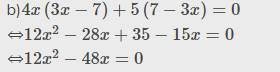
Số 35 của bạn đâu rồi với lại -28 -15 = -43 mà
c,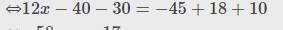
12x - 40x - 30 x
d, chỗ điều kiện xác định dùng dấu \(\left\{{}\begin{matrix}\\\end{matrix}\right.\) này nhé
Với lại bạn chưa đối chiếu