Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

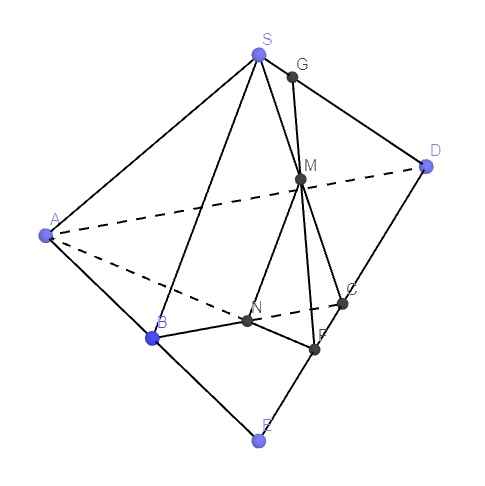
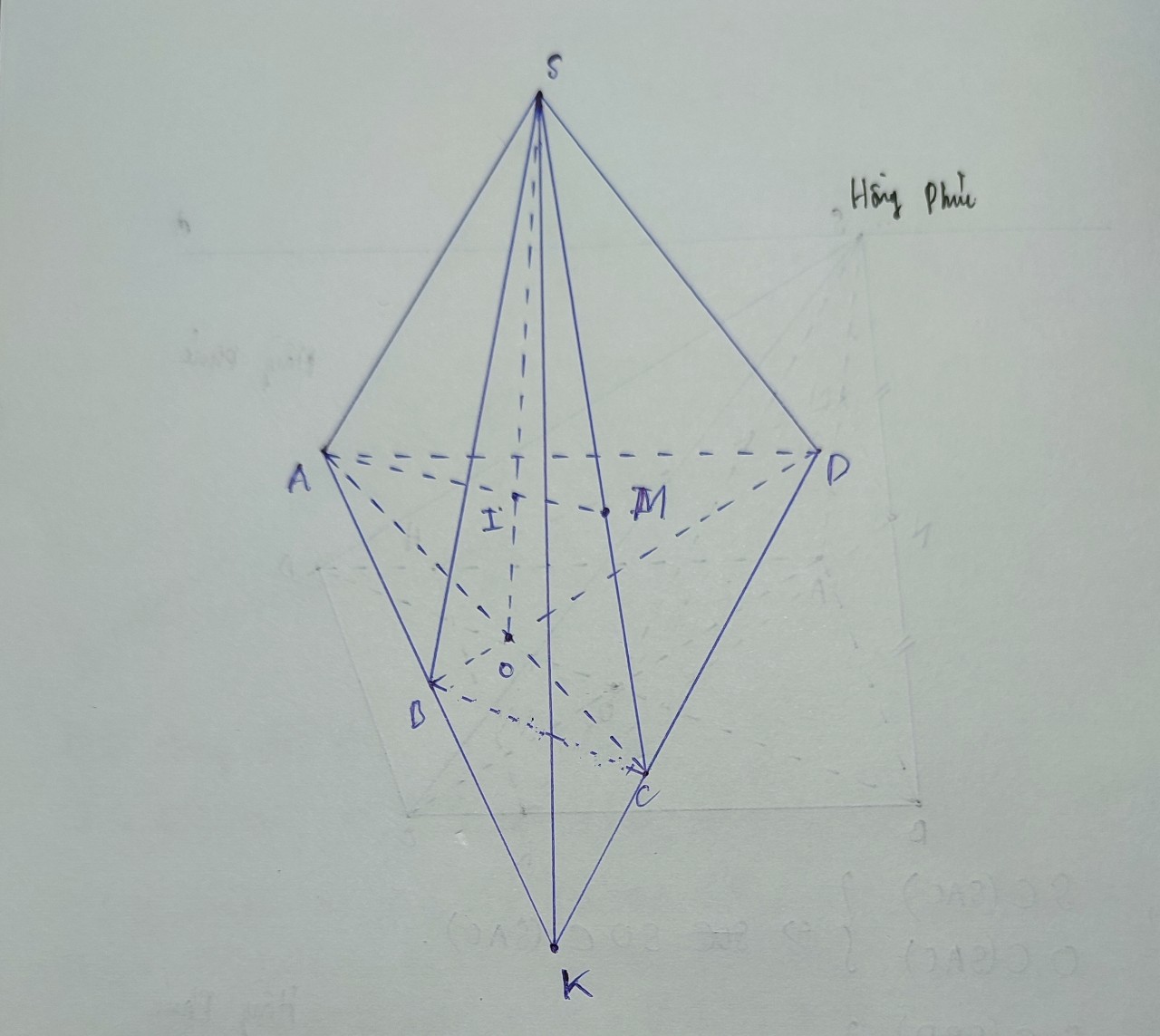
Gọi E là giao điểm AB và CD
\(\Rightarrow E=\left(SAB\right)\cap\left(SCD\right)\)
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
b.
Do M là trung điểm SC, N là trung điểm BC
\(\Rightarrow MN\) là đường trung bình tam giác SBC
\(\Rightarrow MN||SB\)
Mà \(SB\in\left(SBD\right)\Rightarrow MN||\left(SBD\right)\)
c.
Trong mp (ABCD), nối AN cắt CD kéo dài tại F
Trong mp (SCD), nối FM kéo dài cắt SD tại G
\(\Rightarrow G=SD\cap\left(AMN\right)\)

Mình sẽ tóm tắt và giải từng ý nhé.
Đề cho: Hình chóp S.ABCD, đáy ABCD là tứ giác.
M nằm trong tam giác SBC, N nằm trong tam giác SCD.
a) Giao tuyến của (AMN) và (ABCD)
- A thuộc (AMN) và A cũng thuộc đáy (ABCD).
- M thuộc (AMN) nhưng M thuộc cạnh SB nên không nằm trên đáy.
- N thuộc (AMN) nhưng N thuộc cạnh SD cũng không nằm trên đáy.
→ Để tìm giao tuyến, ta cần 2 điểm chung. Điểm A có rồi, điểm thứ hai là giao điểm của MN với đáy (ABCD) nếu có.
Nhưng MN nối M (SB) và N (SD), cả hai không thuộc đáy, nên để tìm điểm đó ta phải xét: SB và SD giao đáy tại B và D, nối BD cắt MN tại một điểm I. I thuộc đáy, I thuộc MN, nên I ∈ (AMN) ∩ (ABCD).
→ Giao tuyến chính là AI.
b) Giao điểm của MN với (SAC)
- M thuộc SB, N thuộc SD, mặt phẳng (SAC) chứa S, A, C.
- SB và SD đều nằm trong (SBD), không phải (SAC), nhưng đường MN có thể cắt (SAC) tại điểm P. Để tìm P, ta tìm giao điểm của MN với đường SC (vì SC nằm trong cả (SAC) và chứa điểm từ M→N theo hướng hợp lý).
c) Giao điểm của SC với (AMN)
- SC nằm trong (SAC).
- Mặt phẳng (AMN) chứa A, M, N. Để tìm giao điểm Q, ta xét SC cắt MN hoặc cắt một đường trong (AMN). Trong trường hợp này SC và MN có thể cắt nhau tại chính điểm P đã tìm ở câu b).
Tóm lại:
a) AI (I là MN ∩ BD)
b) P = MN ∩ (SAC) (thường là trên SC)
c) Cùng điểm P đó
Nếu bạn muốn mình vẽ hình minh họa để nhìn rõ hơn mình có thể làm ngay.
Cho mình xin 1 tick với ạ

OP là đường trung bình tam giác BCD \(\Rightarrow OP//CD\)
Gọi Q là trung điểm SC \(\Rightarrow\) NQ là đường trung bình tam giác SCD \(\Rightarrow NQ//CD//OP\)
\(\Rightarrow NQ=\left(NPO\right)\cap\left(SCD\right)\)
Trong mp (SBD), nối NM kéo dài cắt SB tại G
\(\Rightarrow AG=\left(SAB\right)\cap\left(AMN\right)\)
Trong mp (ABCD), nối PM kéo dài cắt AD tại H
Trong mp (SAD), nối HN cắt SA tại E
\(\Rightarrow E=SA\cap\left(MNP\right)\)
Nhìn đi nhìn lại cũng ko biết ME//PN kiểu gì
Dễ dàng chứng minh EG=EN, mà GM=3MP nên ME không thể song song PN
Gọi F là giao điểm của MP và AB, I là giao điểm MP và CD
Trong mp (SCD), nối IN cắt SC tại J
Thiết diện là đa giác FENJP


P/s: Ngu phần hình ko gian nên chỉ giúp được thế này thôi nhó :)

c: \(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
=>(SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
d: Gọi O là giao của BC và AD
\(O\in BC\subset\left(SBC\right);O\in AD\subset\left(SAD\right)\)
=>\(O\in\left(SBC\right)\cap\left(SAD\right)\)
=>\(\left(SBC\right)\cap\left(SAD\right)=SO\)



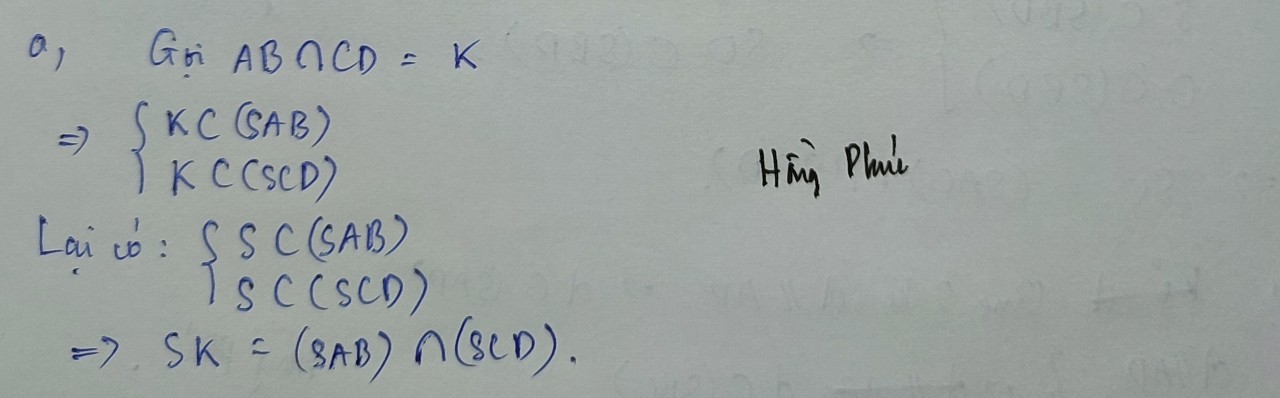

 (BID)
(BID) 