Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{12}=\frac{y}{-8}=\frac{x+y}{12+\left(-8\right)}=\frac{-48}{4}=-12.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=-12\\\frac{y}{-8}=-12\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-144\\y=96\end{cases}}\)
b ) Từ \(x\):\(\left(-7\right)\)= \(y\): \(10\)
\(\Rightarrow\)\(\frac{x}{-7}=\frac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{-7}=\frac{y}{10}=\frac{y-x}{10-\left(-7\right)}=\frac{-34}{17}=-2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-7}=-2\\\frac{y}{10}=-2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=14\\y=-20\end{cases}}\)
c ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{-12}=\frac{2x}{30}=\frac{y}{-12}=\frac{2x+y}{30+\left(-12\right)}=\frac{-360}{18}=-20\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=-20\\\frac{y}{-12}=-20\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-300\\y=240\end{cases}}\)
d ) Từ \(2x=-3y\)\(\Rightarrow\)\(\frac{x}{-3}=\frac{y}{2}\)
Áp dugj tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{-3}=\frac{y}{2}=\frac{x}{-3}=\frac{5y}{10}=\frac{x-5y}{-3-10}=\frac{-130}{-13}=10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{-3}=10\\\frac{y}{2}=10\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-30\\y=20\end{cases}}\)
Bài 2 :
a ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=\frac{x+y-z}{2+\left(-3\right)-5}=\frac{-54}{-6}=9.\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=9\\\frac{y}{-3}=9\\\frac{z}{5}=9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=18\\y=-27\\z=45\end{cases}}\)
b ) Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{-7}=\frac{z}{3}=\frac{x}{4}=\frac{2y}{-14}=\frac{z}{3}=\frac{x+2y-z}{4+\left(-14\right)-3}=\frac{-39}{-13}=3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=3\\\frac{y}{-7}=3\\\frac{z}{3}=3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=12\\y=-21\\z=9\end{cases}}\)

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)


a) Xét tam giác ABM và tam giác ACM:
+ AB = AC (gt).
+ AM chung.
+ \(\widehat{BAM}=\widehat{CAM}\) (AM là phân giác).
\(\Rightarrow\) Tam giác ABM = Tam giác ACM (c - g - c).
b) Xét tam giác ABC: AB = AC (gt).
\(\Rightarrow\) Tam giác ABC cân tại A.
Mà AM là phân giác (gt).
\(\Rightarrow\) AM là trung tuyến; AM là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) M là trung điểm của BC; \(AM\perp BC\) (đpcm).

\(a,\left\{{}\begin{matrix}AB=CD\\AD=BC\\AC\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABC=\Delta CDA\left(c.c.c\right)\\ b,\Delta ABC=\Delta CDA\left(\text{cm trên}\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{BAC}=\widehat{ACD}\Rightarrow AB\text{//}CD\\\widehat{DAC}=\widehat{ACB}\Rightarrow AD\text{//}BC\end{matrix}\right.\)




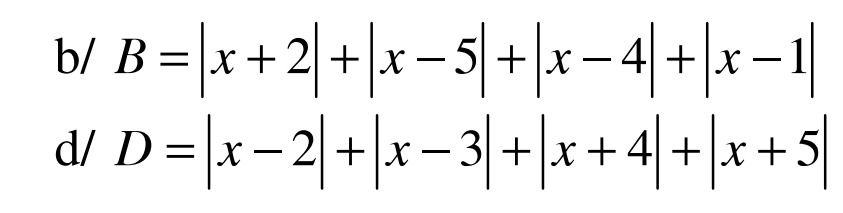

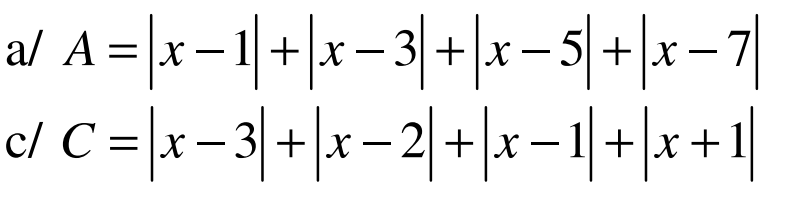



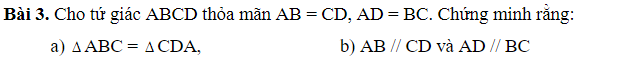
 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
\(14)\)\(\left\{145-\left[130-\left(246-236\right)\right]\div2\right\}.5\)
\(=\)\(\left\{145-\left[130-10\right]\div2\right\}.5\)
\(=\)\(\left\{145-120\div2\right\}.5\)
\(=\)\(\left\{145-60\right\}.5\)
\(=\)\(85.5\)
\(=\)\(425\)
\(15)\)\(325-5.\left[4^3-\left(27-5^2\right)\div1^{2022}\right]\)
\(=\)\(325-5.\left[64-\left(27-25\right)\div1\right]\)
\(=\)\(325-5.\left[64-2\div1\right]\)
\(=\)\(325-5.\left[64-2\right]\)
\(=\)\(325-5.62\)
\(=\)\(325-310\)
\(=\)\(15\)