
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Uh mình chỉ giúp được câu a
\(x^2-5x+3=0\)
\(\Delta=b^2-4ac\)
\(=\left(-5\right)^2-4.1.3\)
\(=25-12=13>0\)
\(x1=\dfrac{b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{13}}{2}\)
\(x2=\dfrac{b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{13}}{2}\)

Hình vẽ : tự vẽ nha
Sabc = \(\frac{1}{2}AH.BC=\frac{1}{2}BK.AC\)
=> \(AH.BC=AC.BK\)
=> \(\frac{AH}{BK}=\frac{AC}{BC}=\frac{15.6}{12}=\frac{13}{10}\)
=> \(\frac{AC}{13}=\frac{BC}{10}=t\)
=> \(AC=13t;BC=10t\)
Tam giác ABC cân có AH là đg cao => AH là t tuyến => BH = HC = 1/2 BC = 1/2.10t = 5t
TAm giác AHC vuông tại H , theo py ta go :
\(AC^2-HC^2=15.6^2\)
=> \(169t^2-25t^2=15.6^2\)
tính ra t thay vào tìm ra BC
2SABC = AH.BC = AC.BK
ð 15,6BC = 12AC
ð BC = 12/15,6AC
ð CH = 6/15,6AC
ð AH2 = AC2 – HC2 = 144/169AC2
ð AH = 12/13 AC
ð 15,6 = 12/13AC
ð AC = 16,9
ð BC = 12/15,6 AC = 13


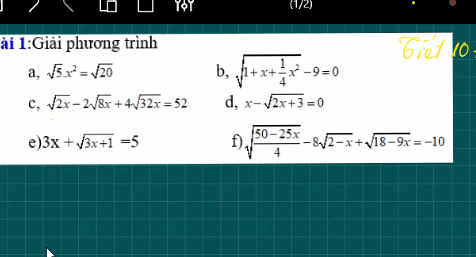
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14

bài 2
a, \(3\sqrt{8}\) + \(\sqrt{18}\) - \(\sqrt{72}\)
=\(6\sqrt{2}\)+\(3\sqrt{2}\)-\(6\sqrt{2}\)
=\(3\sqrt{2}\)(3+1-3)
=3\(\sqrt{2}\)

Hai bài này tương tự nhau, bạn có thể tham khảo nhé.


\(P\ge\dfrac{\left(x+y\right)\left(x+y+z\right)\left(x+y+z+t\right)}{\dfrac{1}{4}\left(x+y\right)^2ztu}=\dfrac{4\left(x+y+z\right)\left(x+y+z+t\right)}{\left(x+y\right)ztu}\)
\(P\ge\dfrac{4\left(x+y+z\right)\left(x+t\text{y}+z+t\right)}{\dfrac{1}{4}\left(x+y+z\right)^2tu}=\dfrac{16\left(x+y+z+t\right)}{\left(x+y+z\right)tu}\)
\(P\ge\dfrac{16\left(x+y+z+t\right)}{\dfrac{1}{4}\left(x+y+z+t\right)^2u}=\dfrac{64}{\left(x+y+z+t\right)u}\ge\dfrac{64}{\dfrac{1}{4}\left(x+y+z+t+u\right)^2}=256\)
Dấu "=" xảy ra khi \(\left(x;y;z;t;u\right)=\left(\dfrac{1}{16};\dfrac{1}{16};\dfrac{1}{8};\dfrac{1}{4};\dfrac{1}{2}\right)\)

a.
\(\Leftrightarrow\dfrac{2a}{2a+b}+\dfrac{2b}{2b+c}+\dfrac{2c}{2c+a}\le2\)
\(\Leftrightarrow\dfrac{2a}{2a+b}-1+\dfrac{2b}{2b+c}-1+\dfrac{2c}{2c+a}-1\le-1\)
\(\Leftrightarrow\dfrac{b}{2a+b}+\dfrac{c}{2b+c}+\dfrac{a}{2c+a}\ge1\)
Thật vậy, ta có:
\(VT=\dfrac{b^2}{2ab+b^2}+\dfrac{c^2}{2bc+c^2}+\dfrac{a^2}{2ca+a^2}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
b.
Chuẩn hóa \(a+b+c=1\), BĐT cần chứng minh trở thành:
\(\dfrac{a}{\left(a+2b\right)^2}+\dfrac{b}{\left(b+2c\right)^2}+\dfrac{c}{\left(c+2a\right)^2}\ge1\)
Ta có:
\(\dfrac{a}{\left(a+2b\right)^2}+a\left(a+2b\right)+a\left(a+2b\right)\ge3a\)
Tương tự:
\(\dfrac{b}{\left(b+2c\right)^2}+b\left(b+2c\right)+b\left(b+2c\right)\ge3b\)
\(\dfrac{c}{\left(c+2a\right)^2}+c\left(c+2a\right)+c\left(c+2a\right)\ge3c\)
Cộng vế:
\(VT+2\left(a+b+c\right)^2\ge3\left(a+b+c\right)\)
\(\Leftrightarrow VT+2\ge3\)
\(\Leftrightarrow VT\ge1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)






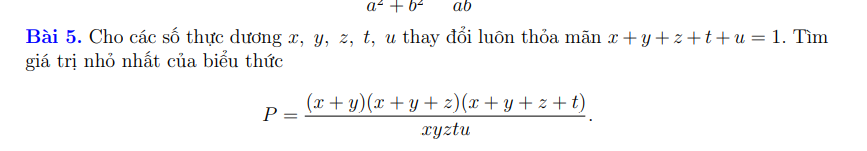












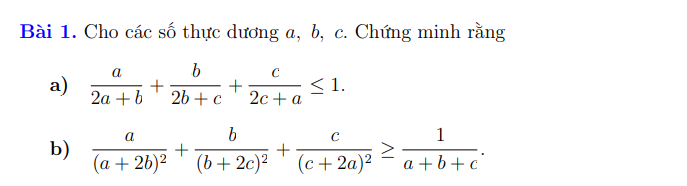
\(\sqrt{x+1}-\sqrt{x-2}=1\)(ĐK: \(x\ge2\))
\(\Leftrightarrow\sqrt{x+1}-2-\sqrt{x-2}+1=0\)
\(\Leftrightarrow\frac{x+1-4}{\sqrt{x+1}+2}-\frac{x-2-1}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\left(x-3\right)\left(\frac{1}{\sqrt{x+1}+2}-\frac{1}{\sqrt{x-2}+1}\right)=0\)
\(\Leftrightarrow x-3=0\)(vì \(\sqrt{x+1}+2>\sqrt{x-2}+1\))
\(\Leftrightarrow x=3\)(thỏa mãn)