Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kệ cái thằng ấy, nó có trả lời đc câu nào tử tế đâu. Câu **** ý mà, kệ nó đi

\(4x^8+1=\)\(4x^8-4x^4+4x^4+1\)\(=\left(4x^8+4x^4+1\right)-4x^4\)
\(=\left(2x^4+1\right)^2-\left(2x^2\right)^2\)\(=\left(2x^4-2x^2+1\right)\left(2x^4-2x^2-1\right)\)
phần b em tự giải nhé

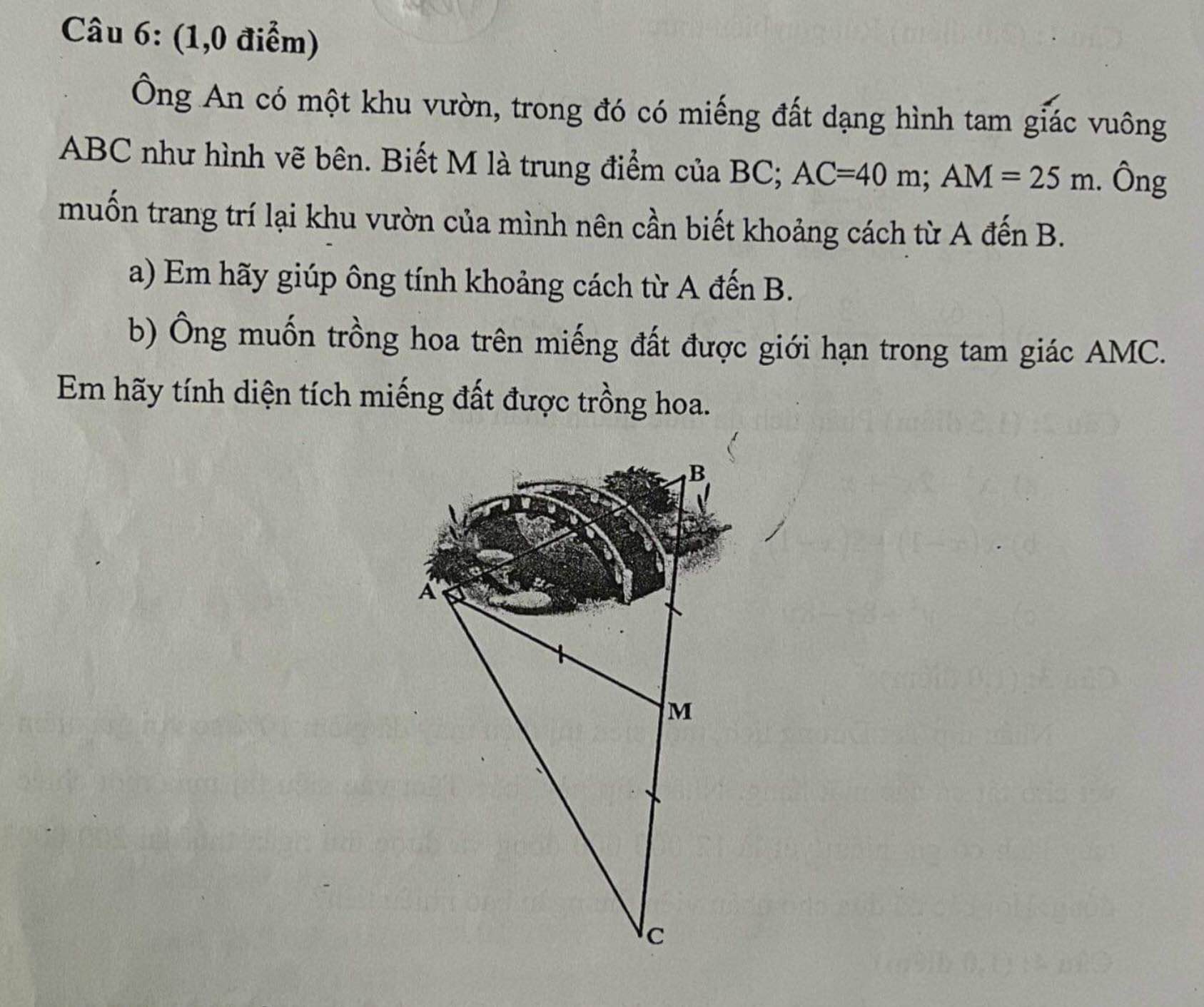
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)

1) \(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)\(\Leftrightarrow\)\(2x^2+2y^2\ge x^2+2xy+y^2\)\(\Leftrightarrow\)\(\left(x-y\right)^2\ge0\) ( luôn đúng )
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y\)
2) \(\frac{1}{xy}=\frac{1}{\left(\sqrt{xy}\right)^2}\ge\frac{1}{\left(\frac{x+y}{2}\right)^2}=4\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=\frac{1}{2}\)
bạn Diệu Linh ơi, bài này bảo chứng minh điều đó là đúng chứ không bảo điều đó là giả thiết nhé bạn, nhưng cũng cảm ơn bạn vì đã giúp mình =))
\(\left(2x-3\right)^2-\left(x-1\right)^2=0\)
=>(2x-3-x+1)(2x-3+x-1)=0
=>(x-2)(3x-4)=0
=>\(\left[\begin{array}{l}x-2=0\\ 3x-4=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\\ 3x=4\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\\ x=\frac43\end{array}\right.\)