
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : |x - 2| ; |x - 5| ; |x - 18| ≥0∀x∈R≥0∀x∈R
=> |x - 2| + |x - 5| + |x - 18| ≥0∀x∈R≥0∀x∈R
=> D có giá trị nhỏ nhất khi x = 2;5;18
Mà x ko thể đồng thời nhận 3 giá trị
Nên GTNN của D là : 16 khi x = 5 ok nha bạn
x^2/x-1 = x^2-4x+4/x-1 + 4 = (x-2)^1/x-1 + 4 >= 4
Dấu "=" xảy ra <=> x-2 = 0 <=> x = 2 (tm)
Vậy GTNN của x^2/x-1 = 4 <=> x= 2
k mk nha



a, ĐKXĐ:\(2x^3-2x^2\ne0\Rightarrow2x^2\left(x-1\right)\ne0\Rightarrow\left\{{}\begin{matrix}2x^2\ne0\\x-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne0\\x\ne1\end{matrix}\right.\)
b, \(A=\dfrac{5x^2-5x}{2x^3-2x^2}\)
\(\Rightarrow A=\dfrac{5x\left(x-1\right)}{2x^2\left(x-1\right)}\)
\(\Rightarrow A=\dfrac{5}{2x}\)
Để A=1\(\Rightarrow\dfrac{5}{2x}=1\)
\(\Rightarrow2x=5\\ \Rightarrow x=\dfrac{5}{2}\)
a, đk \(2x^2\left(x-1\right)\ne0\Leftrightarrow x\ne0;x\ne1\)
b, \(A=\dfrac{5x\left(x-1\right)}{2x^2\left(x-1\right)}=\dfrac{5}{2x}=1\Rightarrow5=2x\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)

a)
\(\left|x\right|=2=>\left[{}\begin{matrix}x=2\\x=-2\left(loaividieukien\right)\end{matrix}\right.\)
thay x=2 vào biểu thức B ta có
\(\dfrac{2\cdot2+2}{2+2}=\dfrac{6}{4}=1,5\)
b)
\(\dfrac{x+1}{2x-2}+\dfrac{1}{2-2x^2}\\ =\dfrac{x+1}{2x-2}-\dfrac{1}{2x^2-2}\\ =\dfrac{x+1}{2\left(x-1\right)}-\dfrac{1}{2\left(x-1\right)\left(x+1\right)}\\ =\dfrac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}-\dfrac{1}{2\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x^2+2x+1-1}{2\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x^2+2x}{2\left(x-1\right)\left(x+1\right)}\\ =\dfrac{x\left(x+2\right)}{2\left(x-1\right)\left(x+1\right)}\)
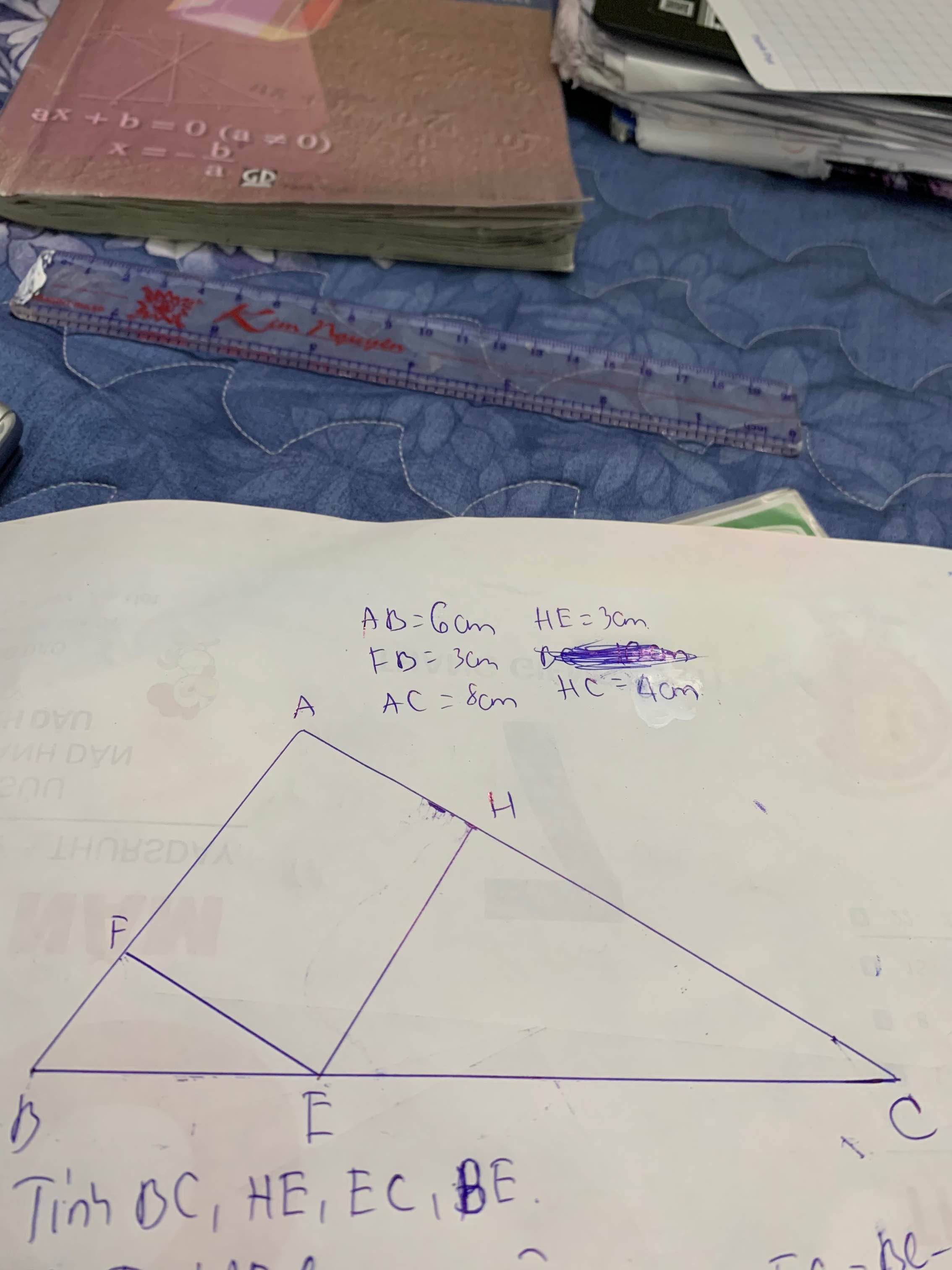
 Mọi người giúp mình với ạ mình cần gấp!!!!!
Mọi người giúp mình với ạ mình cần gấp!!!!!


\(m^2x-3=4x-\left(m+1\right)\)
\(\Leftrightarrow\left(m^2-4\right)x=2-m\)
a. Phương trình có nghiệm \(x=1\) khi:
\(m^2-4=2-m\Rightarrow m^2+m-6=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)
b. Phương trình có vô số nghiệm khi:
\(\left\{{}\begin{matrix}m^2-4=0\\2-m=0\end{matrix}\right.\) \(\Rightarrow m=2\)