K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PV
4
PP
1
8 tháng 12 2021
\(ĐK:x\ne\dfrac{1}{2};x\ne1;x\ne\dfrac{3}{2};x\ne2;x\ne\dfrac{5}{2}\\ PT\Leftrightarrow\dfrac{1}{\left(2x-1\right)\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(3x-2\right)}+\dfrac{1}{\left(3x-2\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(5x-2\right)}=\dfrac{4}{21}\\ \Leftrightarrow2\left[\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{1}{2}\right)\left(x-1\right)}+\dfrac{\dfrac{1}{2}}{\left(x-1\right)\left(x-\dfrac{3}{2}\right)}+\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{3}{2}\right)\left(x-2\right)}+\dfrac{\dfrac{1}{2}}{\left(x-2\right)\left(x-\dfrac{5}{2}\right)}\right]=\dfrac{4}{21}\)
\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{1}{2}}+\dfrac{1}{x-\dfrac{3}{2}}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-\dfrac{3}{2}}+\dfrac{1}{x-\dfrac{5}{2}}-\dfrac{1}{x-2}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{x-\dfrac{5}{2}-x+1}{\left(x-1\right)\left(x-\dfrac{5}{2}\right)}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{-\dfrac{3}{2}}{x^2-\dfrac{7}{2}x+\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow x^2-\dfrac{7}{2}x+\dfrac{5}{2}=-\dfrac{63}{4}\\ \Leftrightarrow4x^2-14x+10=-63\\ \Leftrightarrow4x^2-14x+73=0\\ \Leftrightarrow x\in\varnothing\)
HD
1
H
13 tháng 12 2022
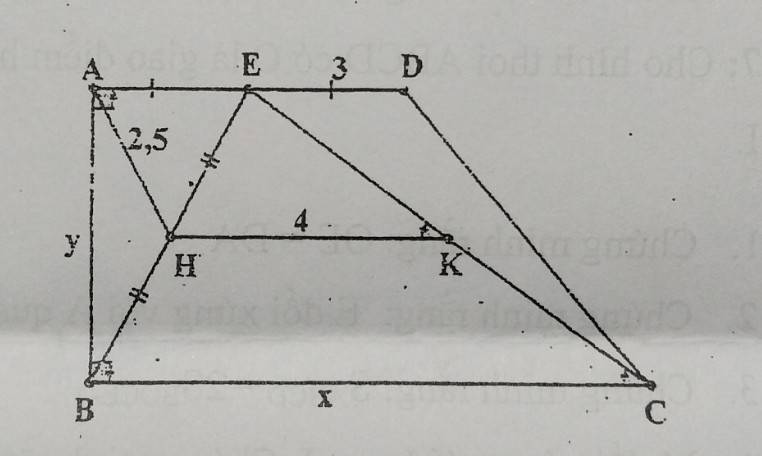
Có: ∠EKH = ∠KCB
Mà 2 góc ở vị trí đồng vị
⇒ HK // BC
Xét △EBC có:
H trung điểm EB
HK // BC
⇒ HK đường trung bình
⇒ HK = \(\dfrac{1}{2}\)BC
⇒ BC = 2HK
⇒ x = 2 . 4 = 8
Xét △AEB ⊥ A, có:
AH đường trung tuyến (H trung điểm EB)
⇒ AH = \(\dfrac{1}{2}\)EB
⇒ EB = 2AH = 2 . 2,5 = 5
Vì AE = ED
Mà ED = 3
⇒ AE = 3
Áp dụng định lý Pytago vào △AEB ⊥ A
⇒ \(EB^2=AE^2+AB^2\)
⇒ AB = y = \(\sqrt{BE^2-AE^2}\) = \(\sqrt{5^2-3^2}\) = \(4\)
Vậy x = 8 và y = 4
31 tháng 10 2021
\(4,=3x^2-3x+7x-7=\left(x-1\right)\left(3x+7\right)\\ 5,=4x^2-4xy+9xy-9y^2=\left(x-y\right)\left(4x+9y\right)\\ 6,=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)=\left(x+2y\right)\left(x-2y-2\right)\)
31 tháng 10 2021
1: \(x^2+2x-3=\left(x+3\right)\left(x-1\right)\)
2: \(x^2+3x-10=\left(x+5\right)\left(x-2\right)\)
3: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
NK
0
HG
2
8 tháng 12 2023
Cái này dùng HĐT số 3 á bạn
\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
8 tháng 12 2023
Bạn áp dụng hằng đẳng thức A2-B2=(A-B).(A+B) nha
(2x-5)2-(3x-4)2=[(2x-5)+(3x-4)].[(2x-5)-(3x-4)]
=(2x-5+3x-4).(2x-5-3x+4)
=(2x-5-3x+4).(2x-5+3x-4)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
\(2x\left(x^2+1\right)-2x^2\left(x+1\right)=0\)
\(\Leftrightarrow2x^3+2x-2x^3-2x^2=0\)
\(\Leftrightarrow2x-2x^2=0\)
\(\Leftrightarrow2x\left(1-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\1-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
18 tháng 8 2021
b,2x(x^2+1)-2x^2(x+1)=0
<=>2x^3+2x-2x^3-2x^2=0
<=>2x-2x^2=0
<=>2x(1-x)=0
<=>2x=0 hoặc 1-x=0
<=>x=0 hoặc x=1
NT
1
30 tháng 12 2021
a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)
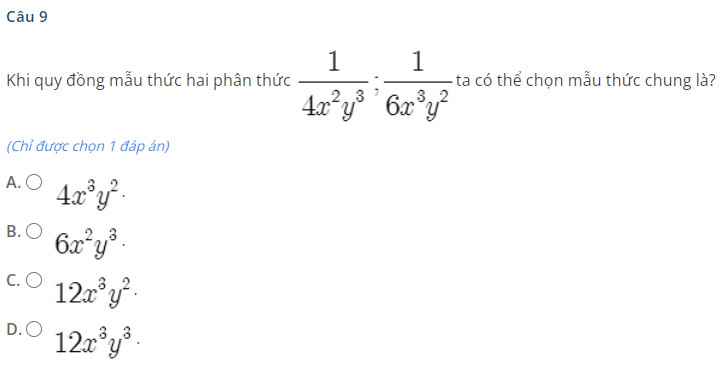
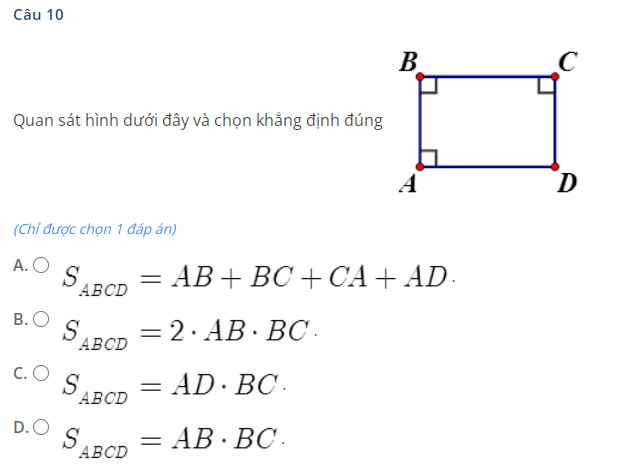
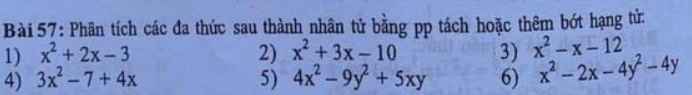
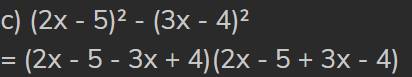
4x2y3=2x2.2y2.y
6x3y2=2.3.x2y2.x
=> MTC= 2.2.3.x3y3=12x3y3
4x2y3=2x2.2y2.y
6x3y2=2.3.x2y2.x
=> MTC= 2.2.3.x3y3=12x3y3