
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=1\Rightarrow y=0\\x=-1\Rightarrow y=0\end{matrix}\right.\)
\(\Rightarrow A\left(0;1\right);B\left(1;0\right);C\left(-1;0\right)\)
\(S=\dfrac{1}{2}.\left|y_A-y_B\right|.\left|x_B-x_C\right|=\dfrac{1}{2}.1.2=1\)


\(y'=\left(2m+1\right)\cos x+3-m\)
Hàm số đã cho đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow\left(2m+1\right)\cos x\le m-3\) (1)
*TH: \(2m+1< 0\Leftrightarrow m< \frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\ge\frac{m-3}{2m+1}\) (không thoả với mọi x)
*TH: \(2m+1>0\Leftrightarrow m>\frac{-1}{2}\), ta có
\(\left(1\right)\Leftrightarrow\cos x\le\frac{m-3}{2m+1}\) (2)
(2) đúng với mọi x khi và chỉ khi \(\left|\frac{m-3}{2m+1}\right|>1\Leftrightarrow\left[\begin{array}{nghiempt}m< -4\\m>\frac{2}{3}\end{array}\right.\)
kết hợp \(m>\frac{-1}{2}\) ta có m > 3/2 là giá trị cần tìm

Bài 1:
Vì $a\geq 1$ nên:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}=a+\sqrt{(a-1)^2+4}+\sqrt{a-1}\)
\(\geq 1+\sqrt{4}+0=3\)
Ta có đpcm
Dấu "=" xảy ra khi $a=1$
Bài 2:
ĐKXĐ: x\geq -3$
Xét hàm:
\(f(x)=x(x^2-3x+3)+\sqrt{x+3}-3\)
\(f'(x)=3x^2-6x+3+\frac{1}{2\sqrt{x+3}}=3(x-1)^2+\frac{1}{2\sqrt{x+3}}>0, \forall x\geq -3\)
Do đó $f(x)$ đồng biến trên TXĐ
\(\Rightarrow f(x)=0\) có nghiệm duy nhất
Dễ thấy pt có nghiệm $x=1$ nên đây chính là nghiệm duy nhất.

a. Để hàm số đã cho có một cực trị thì -m(2m-1)>0 \(\Rightarrow\) 0<m<1/2.
b. Để hàm số đã cho có ba cực trị thì -m(2m-1)<0 \(\Rightarrow\) m<0 hoặc m>1/2.
c. Để hàm số đã cho có một cực trị là cực đại thì m<0 và -(2m-1)<0, suy ra không có giá trị nào của m thỏa yêu cầu của bài toán.


Câu 1:
PT hoành độ giao điểm: $3^{x^2+1}=5$
$x^2+1=\log_35$
$\Leftrightarrow x^2=\log_35-1>0$
$\Rightarrow$ pt hoành độ giao điểm có 2 nghiệm
$\Rightarrow$ có 2 giao điểm giữa 2 đths. Đáp án C.
Câu 2:
$4^{x^2-x}+2^{x^2-x+1}=3$
$\Leftrightarrow (2^{x^2-x})^2+2.2^{x^2-x}-3=0$
$\Leftrightarrow t^2+2t-3=0$ (đặt $2^{x^2-x}=t$)
$\Leftrightarrow (t-1)(t+3)=0$
$\Rightarrow t=1$ (do $t>0$)
$\Leftrightarrow 2^{x^2-x}=1\Leftrightarrow x^2-x=0$
$\Rightarrow x=0$ hoặc $x=1$
$\Rightarrow |x_1-x_2|=1$
Đáp án D.
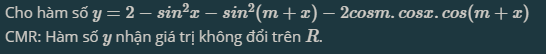





\(y=2-sin^2x-sin^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\)
\(=cos^2x+cos^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\)
\(=cos^2x+\left[cos\left(m+x\right)-2cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x+\left[cosm.cosx-sinm.sinx-2cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x-\left[sinm.sinx+cosm.cosx\right].cos\left(m+x\right)\)
\(=cos^2x-cos\left(m-x\right).cos\left(m+x\right)\)
\(=cos^2x-\dfrac{1}{2}\left(cos2m+cos2x\right)\)
\(=cos^2x-\dfrac{1}{2}cos2x-\dfrac{1}{2}cos2m\)
\(=cos^2x-\dfrac{1}{2}\left(2cos^2x-1\right)-\dfrac{1}{2}cos2m\)
\(=\dfrac{1}{2}-\dfrac{1}{2}cos2m\)
\(\Rightarrow\) Hàm số \(y=2-sin^2x-sin^2\left(m+x\right)-2cosm.cosx.cos\left(m+x\right)\) nhận giá trị không đổi trên R.
Chỉ mình cách giải vớii - Hoc24