Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

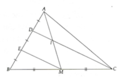
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI

Hình thì tự vẽ nha :))
Nối EM lại .
Có EM là đường trung bình của \(\Delta ABC\)
=> EM // DC
Lại có : DI cắt AE tại trung điểm D
và : EM // DI (EM // DC)
=> DI là đường trung bình của \(\Delta AEM\)
=> DI cắt AM tại trung điểm I
=> IA = IM

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a:Xét ΔBDC có
M là trung điểm của BC
ME//DC
DO đó: E là trung điểm của DB
=>DE=EB(1)
Xét ΔAEM có
I là trung điểm của AM
ID//EM
Do đó: D là trung điểm của AE
=>AD=DE(2)
Từ (1) và (2) suy ra AD=DE=EB
b: Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình
=>ME=CD/2
Xét ΔAEM có
I là trung điểm của AM
D là trung điểm của AE
Do đó: ID là đường trung bình
SUy ra: \(ID=\dfrac{ME}{2}=\dfrac{CD}{2}:2=\dfrac{CD}{4}\)

Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM
