DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)
TN
10 giờ trước (15:44)
Mình nhìn rõ biểu thức trong ảnh là:
$$
V = \sqrt[3]{\,(x^2 - 4)^2\,}.
$$
---
### Phân tích:
* Đây là căn bậc 3 của $(x^2 - 4)^2$.
* Vì căn bậc 3 **luôn xác định với mọi số thực**, nên biểu thức có **tập xác định** là $\mathbb{R}$ (tất cả số thực).
---
### Biến đổi đơn giản hơn:
$$
V = \sqrt[3]{(x^2 - 4)^2} = \big|x^2 - 4\big|^{\tfrac{2}{3}}.
$$
---
✅ Kết luận:
* Tập xác định: $D = \mathbb{R}$.
* Dạng đơn giản: $V = |x^2 - 4|^{2/3}$.
PT
25 tháng 5 2016
bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với
PD
0
NL
0
UH
1
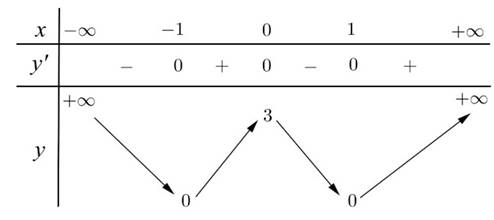
a) Đồ thị hàm số \(y=f\left(x+1\right)\) tạo thành bằng cách tịnh tiến đồ thị hàm số \(y=f\left(x\right)\) sang trái 1 đơn vị nên \(y=f\left(x+1\right)\) đồng biến trên khoảng \(\left(a-1;b-1\right)\) -> Sai
b) Đồ thị hàm số \(y=-f\left(x\right)-1\) tạo thành bằng cách lấy đối xứng đồ thị hàm số \(y=f\left(x\right)\) qua trục Ox và tịnh tiến xuống dưới 1 đơn vị nên hàm số \(y=-f\left(x\right)-1\) nghịch biến trên \(\left(a;b\right)\) -> Đúng.
c) Lập luận tương tự câu b -> c Đúng.
d) Đồ thị hàm số \(y=f\left(x\right)+1\) tạo thành bằng cách tịnh tiến đồ thị hàm số \(y=f\left(x\right)\) lên trên 1 đơn vị nên hàm số \(y=f\left(x\right)+1\) đồng biến trên \(\left(a;b\right)\) -> Đúng.