Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
người giúp em bài này được không ạ ....
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2
a) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{CAD}\) là góc nội tiếp chắn \(\stackrel\frown{CD}\)
mà \(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
nên \(\stackrel\frown{BD}=\stackrel\frown{CD}\)
hay BD=CD
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BD=CD(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD\(\perp\)BC(đpcm)
a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp
a: góc AED+góc AFD=180 độ
=>AEDF nội tiếp
=>góc AEF=góc ADF=góc C
=>góc FEB+góc FCB=180 độ
=>FEBC nội tiếp
b: Xét ΔGBE và ΔGFC có
góc GBE=góc GFC
góc G chung
=>ΔGBE đồng dạng với ΔGFC
=>GB/GF=GE/GC
=>GB*GC=GF*GE
Bài 3:
Gọi K là giao của AH và BC thì AK là đường cao thứ 3 (H là trực tâm)
Vì \(\widehat{BDC}=\widehat{BEC}=90^0\) nên BEDC nội tiếp
Lại có \(BI=IC=ID=IE=\dfrac{1}{2}BC\) (trung tuyến ứng cạnh huyền) nên I là tâm đg tròn ngoại tiếp BDEC
Gọi G là trung điểm AH thì \(AG=GD=DE=\dfrac{1}{2}AH\) (trung tuyến ứng ch)
Do đó G là tâm () ngoại tiếp tg ADE
Vì \(GA=GD\Rightarrow\widehat{DAG}=\widehat{GDA}\)
Vì \(ID=IB\Rightarrow\widehat{ABI}=\widehat{IDB}\)
Do đó \(\widehat{IDB}+\widehat{GDA}=\widehat{DAG}+\widehat{ABI}=90^0\left(\Delta AKB\perp K\right)\)
Do đó \(\widehat{IDG}=180^0-\left(\widehat{IDB}+\widehat{GDA}\right)=90^0\)
Vậy \(ID\perp IG\) hay ...
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
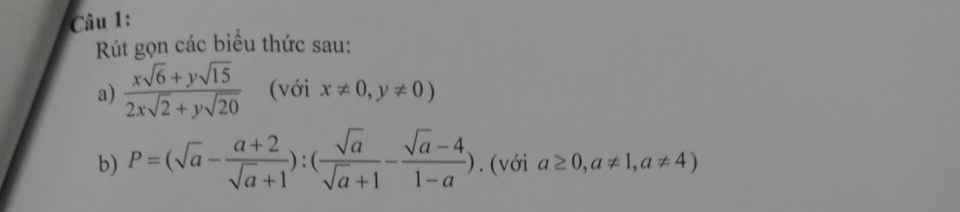
Từ câu a ta có AE=AF \(\Rightarrow\Delta AEF\) vuông cân tại A
\(\Rightarrow AI\) đồng thời là phân giác \(\widehat{FAE}\Rightarrow\widehat{KAF}=\dfrac{1}{2}\widehat{FAE}=\dfrac{1}{2}.90^0=45^0\)
Lại có ABCD là hình vuông \(\Rightarrow\widehat{ACF}=45^0\)
\(\Rightarrow\widehat{ACF}=\widehat{KAF}\)
Xét hai tam giác AKF và CAF có: \(\left\{{}\begin{matrix}\widehat{ACF}=\widehat{KAF}\\\widehat{AFC}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AKF\sim\Delta CAF\left(g.g\right)\Rightarrow\dfrac{AF}{CF}=\dfrac{FK}{AF}\Rightarrow AF^2=KF.CF\)