
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(P=\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{9}+5}{\sqrt{9}-2}=\dfrac{3+5}{3-2}=8\)
b) \(Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{5\sqrt{x}-2}{4-x}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-3\sqrt{x}+2+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
c) \(M=\dfrac{Q}{P}=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+5}=\dfrac{\sqrt{x}}{\sqrt{x}+5}< \dfrac{1}{2}\)
\(\Leftrightarrow2\sqrt{x}< 3\sqrt{x}+15\Leftrightarrow\sqrt{x}>-15\left(đúng\forall x\ge0,x\ne4\right)\)
d) \(M=\dfrac{\sqrt{x}}{\sqrt{x}+5}=1-\dfrac{5}{\sqrt{x}+5}\in Z\)
\(\Rightarrow\sqrt{x}+5\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(x\ge0,x\ne4\)
\(\Rightarrow x\in\left\{0\right\}\)


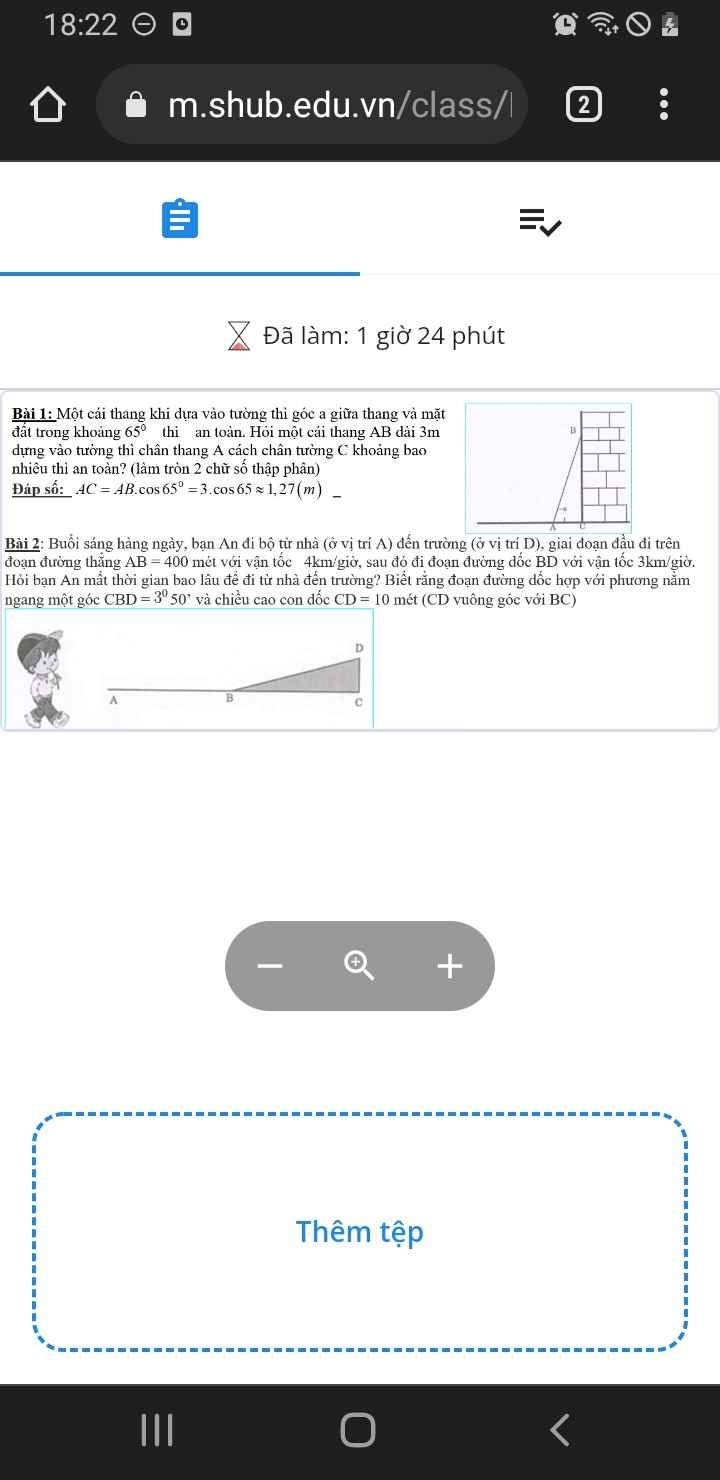
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)


Bài 1:
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)

Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc 1 đường tròn(1)
Xét tứ giác OHAC có
\(\widehat{OHA}+\widehat{OCA}=180^0\)
Do đó: OHAC là tứ giác nội tiếp
=>O,H,A,C cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,B,H,O,C cùng năm trên 1 đường tròn
b: \(\widehat{BHA}=\widehat{BOA}\)
\(\widehat{CHA}=\widehat{AOC}\)
mà \(\widehat{AOB}=\widehat{AOC}\)
nên \(\widehat{BHA}=\widehat{CHA}\)
hay HA là tia phân giác của góc BHC




 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
 Mọi người giúp em với, em cần gấp lắm rồi :((
Mọi người giúp em với, em cần gấp lắm rồi :((
Bài 9:
a) \(P=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\) (ĐK: \(x\ne1;x\ne4;x>0\))
\(P=\left[\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left[\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right]\)
\(P=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\)
\(P=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\)
\(P=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(P=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b) \(P>\dfrac{1}{6}\) khi
\(\Rightarrow\dfrac{\sqrt{a}-2}{3\sqrt{a}}>\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{\sqrt{a}-2}{3\sqrt{a}}-\dfrac{1}{6}>0\)
\(\Leftrightarrow\dfrac{2\left(\sqrt{a}-2\right)-\sqrt{a}}{2\cdot3\sqrt{a}}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{a}-4-\sqrt{a}}{6\sqrt{a}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{a}-4}{6\sqrt{a}}>0\)
Mà: \(6\sqrt{a}>0\)
\(\Leftrightarrow\sqrt{a}-4>0\)
\(\Leftrightarrow\sqrt{a}>4\)
\(\Leftrightarrow a>16\)
Vậy: ...
20:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >1\end{matrix}\right.\)
\(P=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{1-\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\cdot2\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\left(\sqrt{x}+1\right)\cdot\sqrt{x}+1>=1>0\)
2>0
Do đó: \(P=\dfrac{2}{x+\sqrt{x}+1}>0\)
8:
a: ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a< >1\end{matrix}\right.\)
\(P=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{\left(a-1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{a-1}\)
\(=\dfrac{a-1}{4a}\cdot\left(-4\sqrt{a}\right)=-\dfrac{a-1}{\sqrt{a}}\)
b: P<0
=>\(-\left(a-1\right)< 0\)
=>a-1>0
=>a>1
c: P=-2
=>\(\dfrac{a-1}{\sqrt{a}}=2\)
=>\(a-1=2\sqrt{a}\)
=>\(a-2\sqrt{a}-1=0\)
=>\(\left[{}\begin{matrix}\sqrt{a}=1+\sqrt{2}\left(nhận\right)\\\sqrt{a}=1-\sqrt{2}\left(loại\right)\end{matrix}\right.\Leftrightarrow a=3+2\sqrt{2}\)