
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
b: ΔOCE cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CE tại K
Xét tứ giác OAMK có \(\widehat{OAM}+\widehat{OKM}=90^0+90^0=180^0\)
nên OAMK là tứ giác nội tiếp
=>O,A,M,K cùng thuộc một đường tròn
c: Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là tiếp tuyến
Do đó: MO là phân giác của \(\widehat{AMB}\)
MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=30^0\cdot2=60^0\)
ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=OM^2-OA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(AM=R\sqrt{3}\)
Xét ΔAMB có MA=MB và \(\widehat{AMB}=60^0\)
nên ΔMAB đều
=>\(S_{MAB}=MA^2\cdot\dfrac{\sqrt{3}}{4}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)

\(\sqrt{16+6\sqrt{7}}=\sqrt{9+2.3.\sqrt{7}+7}=\sqrt{\left(3+\sqrt{7}\right)^2}=\left|3+\sqrt{7}\right|=3+\sqrt{7}\)
\(\sqrt{16+6\sqrt{7}}=\sqrt{9+2.3\sqrt{7}+7}=\sqrt{3^2+2.3\sqrt{7}+\left(\sqrt{7}\right)^2}\)\(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)


\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...

Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2

Gọi tuổi của Minh là x
=>Tuổi của Ninh là x+2
Tuổi của Lan là 1/2x
Theo đề, ta co: 1/2x+x+2+x=27
=>2,5x=25
=>x=10

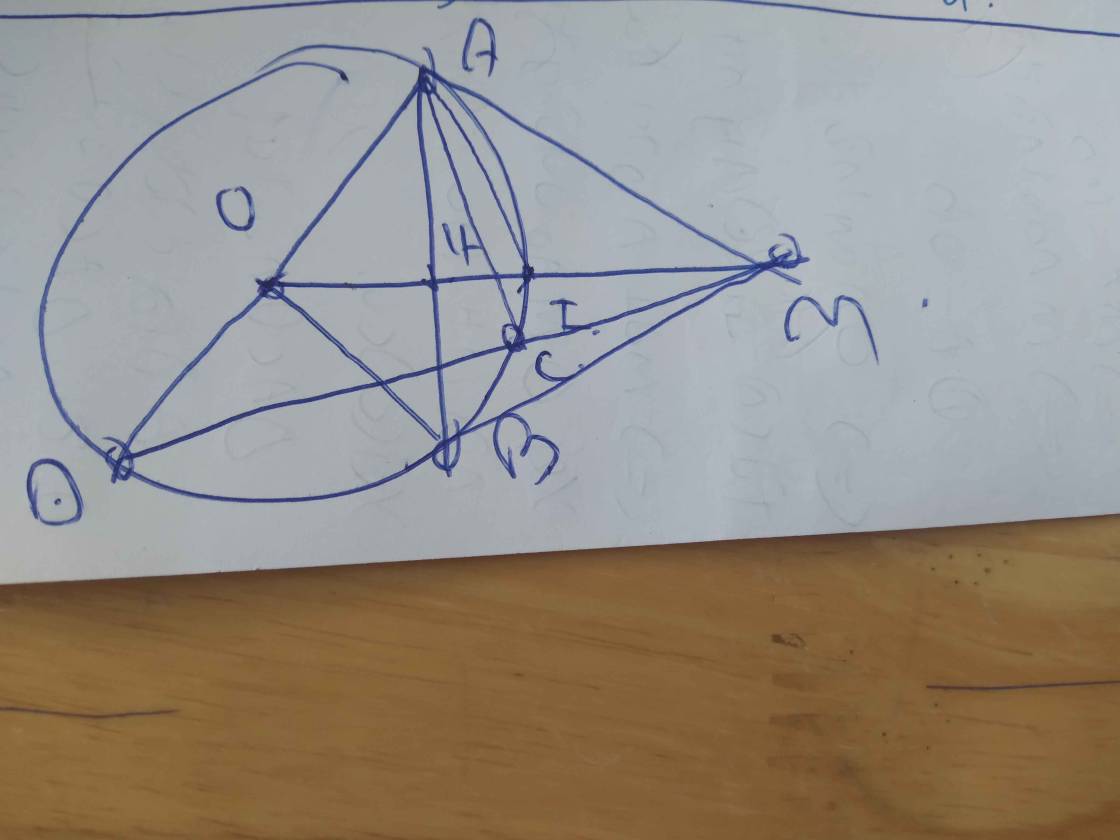
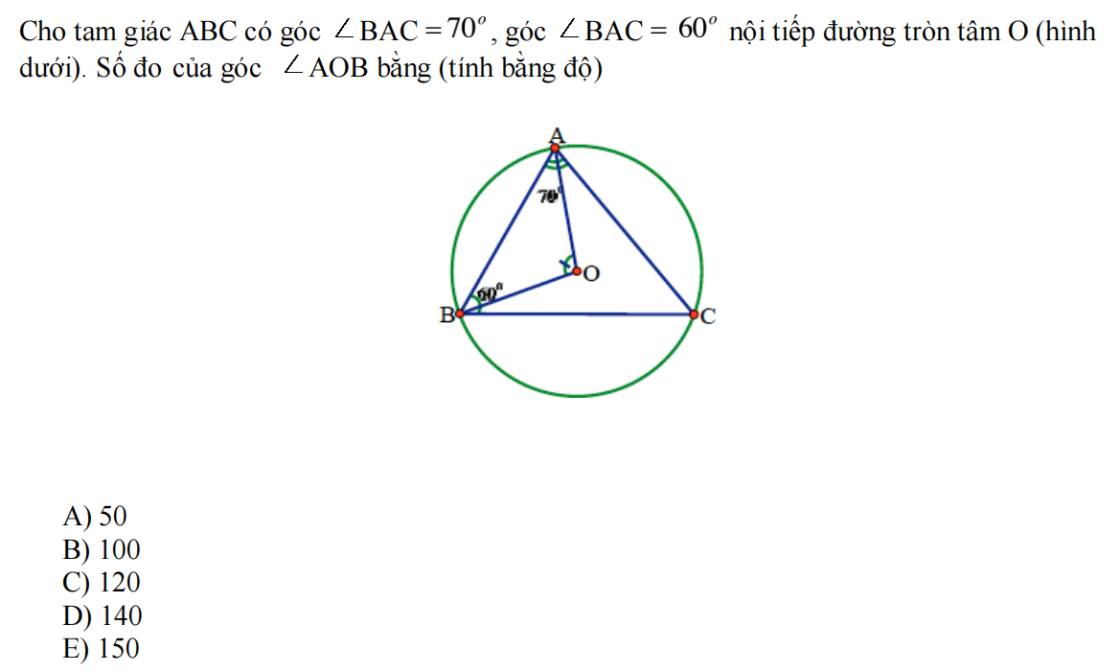
\(\widehat{ACB}=180^0-\left(\widehat{BAC}+\widehat{ABC}\right)=50^0\)
\(\Rightarrow\widehat{AOB}=2.\widehat{ACB}=100^0\) (góc ở tâm gấp đôi góc nội tiếp chắn cùng dây cung)




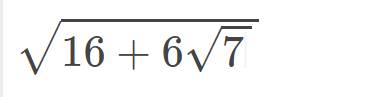 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ










\(\left(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\right)^2\)
\(=4-\sqrt{7}-2\sqrt{16-7}+4+\sqrt{7}=8-2.3=2\)