LD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mọi người giải rõ ràng ra dùm mình với
8 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{36}=\dfrac{b}{38}=\dfrac{a+b}{36+38}=\dfrac{222}{74}=3\)
Do đó: a=108; b=114
8 tháng 1 2022
\(\text{Gọi x;y lần lượt là số dây đeo khẩu trang lớp 7A,7B:}\)
(đk:x;y\(\in\)N*,đơn vị:dây đeo khẩu trang)
\(\text{Ta có:}\dfrac{x}{36}=\dfrac{y}{38}\text{ và }x+y=222\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{36}=\dfrac{y}{38}=\dfrac{x+y}{36+38}=\dfrac{222}{74}=3\)
\(\Rightarrow x=3.36=108\text{(dây đeo khẩu trang)}\)
\(y=3.38=114\text{(dây đeo khẩu trang)}\)
\(\text{Vậy số dây đeo khẩu trang lớp 7A là:108 dây đeo khẩu trang}\)
\(\text{lớp 7B là:114 dây đeo khẩu trang}\)
12 tháng 10 2020
P = 3, 7 + | 4, 3 - x |
Ta có : | 4, 3 - x | ≥ 0 ∀ x
=> 3, 7 + | 4, 3 - x | ≥ 3, 7 ∀ x
Dấu "=" xảy ra <=> 4, 3 - x = 0 => x = 4, 3
=> MinP = 3, 7 <=> x = 4, 3
Q = 5,5 - | 2x - 1, 5 |
Ta có : - | 2x -1, 5 | ≤ 0 ∀ x
=> 5, 5 - | 2x - 1, 5 | ≤ 5, 5 ∀ x
Dấu "=" xảy ra <=> 2x - 1, 5 = 0 => x = 3/4
=> MaxQ = 5, 5 <=> x = 3/4
2P
1
4 tháng 1 2022
b: \(=\dfrac{3}{8}\left(19+\dfrac{1}{3}-33-\dfrac{1}{3}\right)=\dfrac{3}{8}\cdot\left(-14\right)=\dfrac{-42}{8}=\dfrac{-21}{4}\)
c: \(=\dfrac{27}{23}+\dfrac{5}{21}-\dfrac{4}{23}+\dfrac{1}{2}+\dfrac{16}{21}=2+\dfrac{1}{2}=\dfrac{5}{2}\)
d: \(=\dfrac{21+26}{47}+\dfrac{1+4}{5}=2\)
30 tháng 8 2021
Ta có:
x+1xx+1x là số nguyên
⇒x+1⋮x⇒x+1⋮x
⇒1⋮x⇒1⋮x
⇒x∈Ư(1)⇒x∈Ư(1)
⇒x=1 x=−1
mk tin rằng bn đọc rùi sẽ hiểu
Hok tốt
SW
3
9 tháng 11 2018
* Với x < 0
Ta có : |x| + x = -x + x = 0 là số chẵn
*Với x > 0
Ta có : |x| + x = x + x = 2x là số chẵn
Vậy
9 tháng 11 2018
+) Với \(x\ge0\)\(\Rightarrow\)\(\left|x\right|+x=x+x=2x\) ( chẵn )
+) Với \(x< 0\)\(\Rightarrow\)\(\left|x\right|+x=-x+x=0\) ( chẵn )
Vậy \(\forall x\inℤ\) thì \(\left|x\right|+x\) chẵn
...
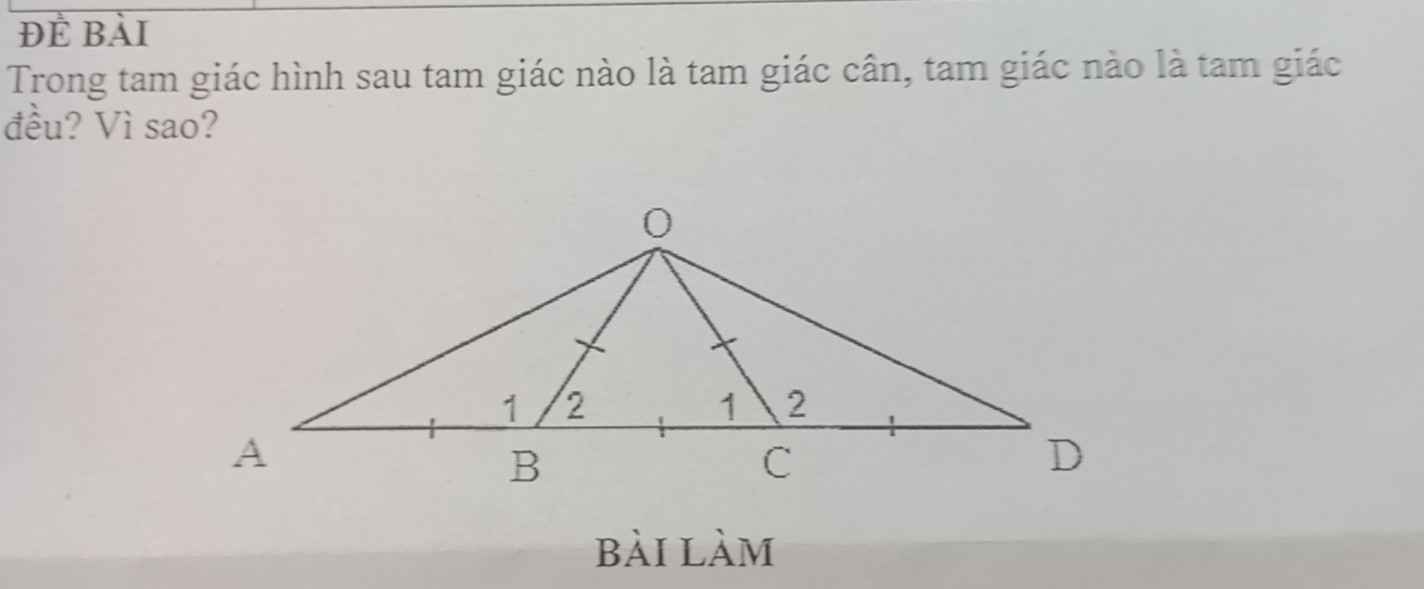
dựng hình bình hành ABFC như hình vẽ.
ta chứng minh \(\Delta AFC=\Delta EDA\)
ta có: AE=CA
CF=AB=DA
\(\widehat{FCA}=\widehat{DAE}\)( do cùng cộng với góc \(\widehat{BAC}=180^0\))
Vậy \(\Delta AFC=\Delta EDA\)(c.g.c)
\(\Rightarrow\widehat{A_1}=\widehat{AED}\)(hai góc tương ứng)
mà \(\widehat{A_1}+\widehat{A_2}=90^0\Rightarrow\widehat{A_2}+\widehat{AED}=90^0\)\(\Rightarrow AM\)vuông góc với DE