Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TA CÓ TAM GIÁC ABC VUÔNG TẠI B , AD ĐL PYTAGO TA CÓ
\(AB^2+BC^2=AC^2\)
=>\(8^2+15^2=289=>AC^{ }=17\)
=>AC=17 CM
A B C E

cau a phai la tamgiac HBA = tamgiac AMD phai k
phai thi tu ve hinh :
a, DM | IH (GT) va AH | BH (GT) ma 2 duong thang DM; BH phan biet
=> DM // BH (dl)
=> goc MDB + DBH = 180o (tcp)
co tamgiac ADB vuong can tai A do goc A = 90o (gt) va AD = AB (gt)
=> goc MDA + goc ABH = 90o
ma goc MDA + goc DAM = 90o (tc) do tamgiac DMA vuong tai M do DM | IA (gt)
=> goc MAD = goc ABH
xet tamgiac AMD va tamgiac BHA co : goc DMA = goc ANB = 90o va AD = AB (GT)
=> tamgiac AMD = tamgiac BHA (ch - gn)

Bài 1: Ta có hình vẽ sau:
B A C M E
a)Xét ΔABM và ΔECM có:
BM = CM (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đỗi đỉnh)
MA = ME (gt)
=> ΔABM = ΔACM (c.g.c) (đpcm)
b) Vì ΔABM = ΔECM (ý a)
=> \(\widehat{MAB}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> AB // CE (đpcm)
Bài 5: Ta có hình vẽ sau:
O A B D C x y E
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
\(\widehat{O}\) : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> \(\widehat{OBC}=\widehat{OAD}\) và \(\widehat{ODA}=\widehat{OCB}\)
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
\(\widehat{OBC}=\widehat{OAD}\) (cm trên)
AC = BD (gt)
\(\widehat{ODA}=\widehat{OCB}\) (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
\(\widehat{OBC}=\widehat{OAD}\) (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
=> OE là phân giác của \(\widehat{xOy}\)

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

\(\text{#TNam}\)
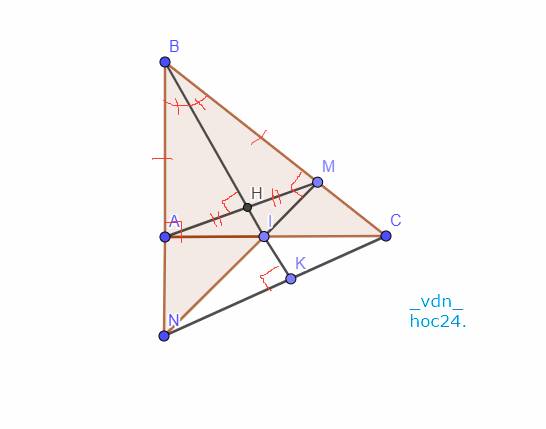
`a,`
Xét Tam giác `ABI` và Tam giác `MBI` có:
`\text {BI chung}`
\(\widehat{ABI}=\widehat{MBI} (\text {tia phân giác}\) \(\widehat{ABM} )\)
\(\widehat{BAI}=\widehat{BMI}=90^0\)
`=> \text {Tam giác ABI = Tam giác MBI (ch-gn)}`
`=> BA = BM (\text {2 cạnh tương ứng})`
Gọi `H` là giao điểm của `BI` với `AM`
Xét Tam giác `HAB` và Tam giác `HMB` có:
\(\text{BA = BM (CMT)}\)
\(\widehat{ABH}=\widehat{MBH} (\text {tia phân giác} \widehat{ABM})\)
`\text {BH chung}`
`=> \text {Tam giác HAB = Tam giác HMB (c-g-c)}`
`-> \text {HA = HM (2 cạnh tương ứng)}`
`->`\(\widehat{BHA}=\widehat{BHM} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BHA}+\widehat{BHM}=180^0\)
`->`\(\widehat{BHA}=\widehat{BHM}=\)`180/2=90^0`
`-> \text {BH} \bot \text {AM}`
Ta có: \(\left\{{}\begin{matrix}BH\perp AM\\HA=HM\end{matrix}\right.\)
`->` \(\text{BI là đường trung trực của AM.}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BMN` có:
\(\widehat{B} \) `\text {chung}`
`BA = BM (a)`
\(\widehat{BAC}=\widehat{BMN}=90^0\)
`=> \text {Tam giác BAC = Tam giác BMN (g-c-g)}`
`-> \text {BN = BC (2 cạnh tương ứng)}`
Xét Tam giác `BIN` và Tam giác `BIC` có:
`BN = BC (CMT)`
\(\widehat{NBI}=\widehat{CBI} (\text {tia phân giác} \widehat{NBC})\)
`\text {BI chung}`
`=> \text {Tam giác BIN = Tam giác BIC (c-g-c)}`
`-> \text {IN = IC (2 cạnh tương ứng)}`
`c,`
Gọi `K` là giao điểm của `BI` và `NC`
Xét Tam giác `NBK` và Tam giác `CBK` có:
`BN = BC (CMT)`
\(\widehat{NBK}=\widehat{CBK} (\text {tia phân giác} \widehat{NBC})\)
`\text {BK chung}`
`=> \text {Tam giác NBK = Tam giác CBK (c-g-c)}`
`->`\(\widehat{BKN}=\widehat{BKC} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BKN}+\widehat{BKC}=180^0\)
`->`\(\widehat{BKN}=\widehat{BKC}=\)`180/2=90^0`
`-> \text {BK} \bot \text {NC}`
`-> \text {BI} \bot \text {NC (đpcm)}`