mog mn giúp em ạ , cảm ơn 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 8 2021
\(\dfrac{-13}{8}+\dfrac{-5}{9}+\dfrac{26}{26}-\dfrac{13}{9}\)
= \(\left(\dfrac{-13}{8}+\dfrac{26}{16}\right)+\left(\dfrac{-5}{9}-\dfrac{13}{9}\right)\)
= \(\left(\dfrac{-26}{16}+\dfrac{26}{26}\right)+\left(\dfrac{-18}{9}\right)\)
= \(0+\left(-2\right)\)
= \(-2\)
4 tháng 8 2021
\(\left(\dfrac{-13}{8}-\dfrac{26}{16}\right)+\left(\dfrac{-5}{9}-\dfrac{13}{9}\right)=\left(\dfrac{-13}{8}-\dfrac{13}{8}\right)+\dfrac{-18}{9}=0+\left(-2\right)=-2\)
9 tháng 9 2021
\(\left(3x-4\right)^3=5^2+4.5^2\)
\(\Leftrightarrow\left(3x-4\right)^3=5^2\left(1+4\right)\)
\(\Leftrightarrow\left(3x-4\right)^3=5^3\)
\(\Leftrightarrow3x-4=5\Leftrightarrow3x=9\Leftrightarrow x=3\)
9 tháng 9 2021
Ta có: \(\left(3x-4\right)^3=5^2+4\cdot5^2\)
\(\Leftrightarrow3x-4=5\)
hay x=3
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
$A=7+(7^2+7^3+7^4+7^5)+(7^6+7^6+7^8+7^9)+....+(7^{2018}+7^{2019}+7^{2020}+7^{2021})$
$=7+7^2(1+7+7^2+7^3)+7^6(1+7+7^2+7^3)+....+7^{2018}(1+7+7^2+7^3)$
$=7+(1+7+7^2+7^3)(7^2+7^6+....+7^{2018}$
$=7+400(7^2+7^6+....+7^{2018})$
Dễ thấy $400(7^2+7^6+....+7^{2018})$ tận cùng là $0$
Do đó $A$ tận cùng là $7$
12 tháng 9 2021
\(3\left(x+2\right)^3-1^{2019}=5\cdot4^2\)
\(\Leftrightarrow3\left(x+2\right)^3=5\cdot16+1=81\)
\(\Leftrightarrow x+2=3\)
hay x=1
MH
12 tháng 9 2021
\(4^{15}.9^{15}< 2^n.3^n< 18^{16}.2^{16}\)
⇒\(\left(4.9\right)^{15}< \left(2.3\right)^n< \left(18.2\right)^{16}\)
⇒\(\left(6^2\right)^{15}< 6^n< \left(6^2\right)^{16}\)
⇒\(6^{30}< 6^n< 6^{32}\)
⇒\(6^n=6^{31}\)
⇒n=31
12 tháng 9 2021
\(4^{15}\cdot9^{15}< 2^n\cdot3^n< 18^{16}\cdot2^{16}\\ \Leftrightarrow\left(4\cdot9\right)^{15}< \left(2\cdot3\right)^n< \left(18\cdot2\right)^{16}\\ \Leftrightarrow36^{15}< 6^n< 36^{16}\\ \Leftrightarrow6^{30}< 6^n< 6^{32}\\ \Leftrightarrow n=31\)
AH
Akai Haruma
Giáo viên
24 tháng 9 2021
Lời giải:
$b=2021^0=1< 26^9=a$
$c=26^9=(2.13)^9=2^9.13^9=(2^3)^3.13^9=8^3.13^9<13^3.13^9$
$=13^{12}< 13^{15}=a$
Vậy $b< c< a$
Đáp án C.
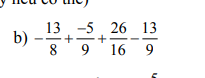
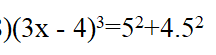
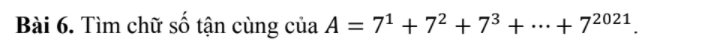
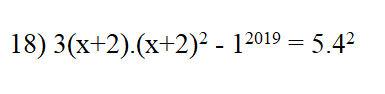
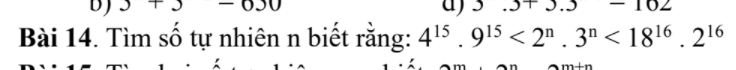
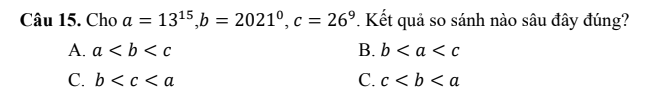
\(a,\\ =\dfrac{10.11+10.5+11.5+10.7+11.7}{11.12+11.5+12.5+11.7+12.7}\\ =\dfrac{10.11\left(1+5.5+7.7\right)}{11.12\left(1+5.5+7.7\right)}=\dfrac{10}{12}=\dfrac{5}{6}\)
\(b,\\ =\dfrac{\left(1.2.3.....25\right).\left(25.26.27....49\right)}{26.27.28.....50}\\ =\dfrac{1.2.3....25}{50}=1.2.3....12\)
cẻm ơn