
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4 :
\(M=\left(2x-3y\right)^2-\left(3y-2\right)\left(3y+2\right)-\left(1-2x\right)^2+4x\left(3y-1\right)\)
\(=\left(2x-3y-1+2x\right)\left(2x-3y+1-2x\right)-9y^2+4+12xy-4x\)
\(=\left(4x-3y-1\right)\left(1-3y\right)-9y^2+4+12xy-4x\)
\(=4x-12xy-3y+9y^2-1+3y-9y^2+4+12xy-4x=3\)
Vậy biểu thức ko phụ thuộc giá trị biến x
Bài 2 :
a, \(\left(a-3b\right)^2=a^2-6ab+9b^2\)
b, \(x^2-16y^4=\left(x-4y^2\right)\left(x+4y^2\right)\)
c, \(25a^2-\frac{1}{4}b^2=\left(5a-\frac{1}{2}b\right)\left(5a+\frac{1}{2}b\right)\)
Bài 3 :
a, \(9x^2-6x+1=\left(3x-1\right)^2\)
b, \(\left(2x+3y\right)^2+2\left(2x+3y\right)+1=\left(2x+3y+1\right)^2\)
c, \(4\left(2x-y\right)^2-8x+4y+1=\left(4x-2y\right)^2-2\left(4x-2y\right)+1=\left(4x-2y-1\right)^2\)

Đề số 3.
1.
a,\(4x\left(5x^2-2x+3\right)\)
\(=20x^3-8x^2+12x\)
b.\(\left(x-2\right)\left(x^2-3x+5\right)\)
\(=x^3-3x^2+5x-2x^2+6x-10\)
\(=x^3-5x^2+11x-10\)
c,\(\left(10x^4-5x^3+3x^2\right):5x^2\)
\(=2x^2-x+\dfrac{3}{5}\)
d,\(\left(x^2-12xy+36y^2\right):\left(x-6y\right)\)
\(=\left(x-6y\right)^2:\left(x-6y\right)\)
\(=x-6y\)
2.
a,\(x^2+5x+5xy+25y\)
\(=\left(x^2+5x\right)+\left(5xy+25y\right)\)
\(=x\left(x+5\right)+5y\left(x+5\right)\)
\(=\left(x+5y\right)\left(x+5\right)\)
b,\(x^2-y^2+14x+49\)
\(=\left(x^2+14x+49\right)-y^2\)
\(=\left(x+7\right)^2-y^2\)
\(=\left(x+7-y\right)\left(x+7+y\right)\)
c,\(x^2-24x-25\)
\(=x^2+25x-x-25\)
\(=\left(x^2-x\right)+\left(25x-25\right)\)
\(=x\left(x-1\right)+25\left(x-1\right)\)
\(=\left(x+25\right)\left(x-1\right)\)
3.
a,\(5x\left(x-3\right)-x+3=0\)
\(5x\left(x-3\right)-\left(x-3\right)=0\)
\(\left(5x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{1}{5}\) hoặc \(x=3\)
b.\(3x\left(x-5\right)-\left(x-1\right)\left(2+3x\right)=30\)
\(3x^2-15x-\left(2x+3x^2-2-3x\right)=30\)
\(3x^2-15x-2x-3x^2+2+3x=30\)
\(-14x+2=30\)
\(-14x=28\)
\(x=-2\)
c,\(\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\)
\(x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\)
\(x^2+5x+6-x^2-5x+2x+10=0\)
\(2x+16=0\)
\(2x=-16\)
\(x=-8\)
Mình học chật hình không giúp bạn được.Xin lỗi!

Câu 4:
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(A=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Để A=-3 thì x-1=-6
hay x=-5(loại)

52 + 122 =132 => tg vuong
Sabc = 12.5/2 = 30cm2
( toán violympic cho rất thông minh, mới nhìn là mk phát hiện ra r , thui mk đi học đây)
Tam giác ABC có 3 cạnh của tam giác ứng với định lí Py-ta-go=> ABC là tam giác vuông
\(S_{ABC}=\frac{5.12}{2}=30cm^2\)

Bài 4:
a) (2x)2-2.2x.(3/2)+(3/2)2=(2x-3/2)2
b) 4(x2+2x+1)-12x-3=4x2-4x+1=(2x)2-2.2x.1+12=(2x-1)2
c) (5x)2-2.5x.2y+(2y)2=(5x-2y)2
Bài 5:
a) (x+3)3
b)[ \(\left[\left(\sqrt{3}x\right)+2\right]^3\)]
c) (3x+31)3
d) \(\left[x+\sqrt{2}y\right]^3\)

Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
mà AC=BD
nên BE=BD
hay ΔBED cân tại B

Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

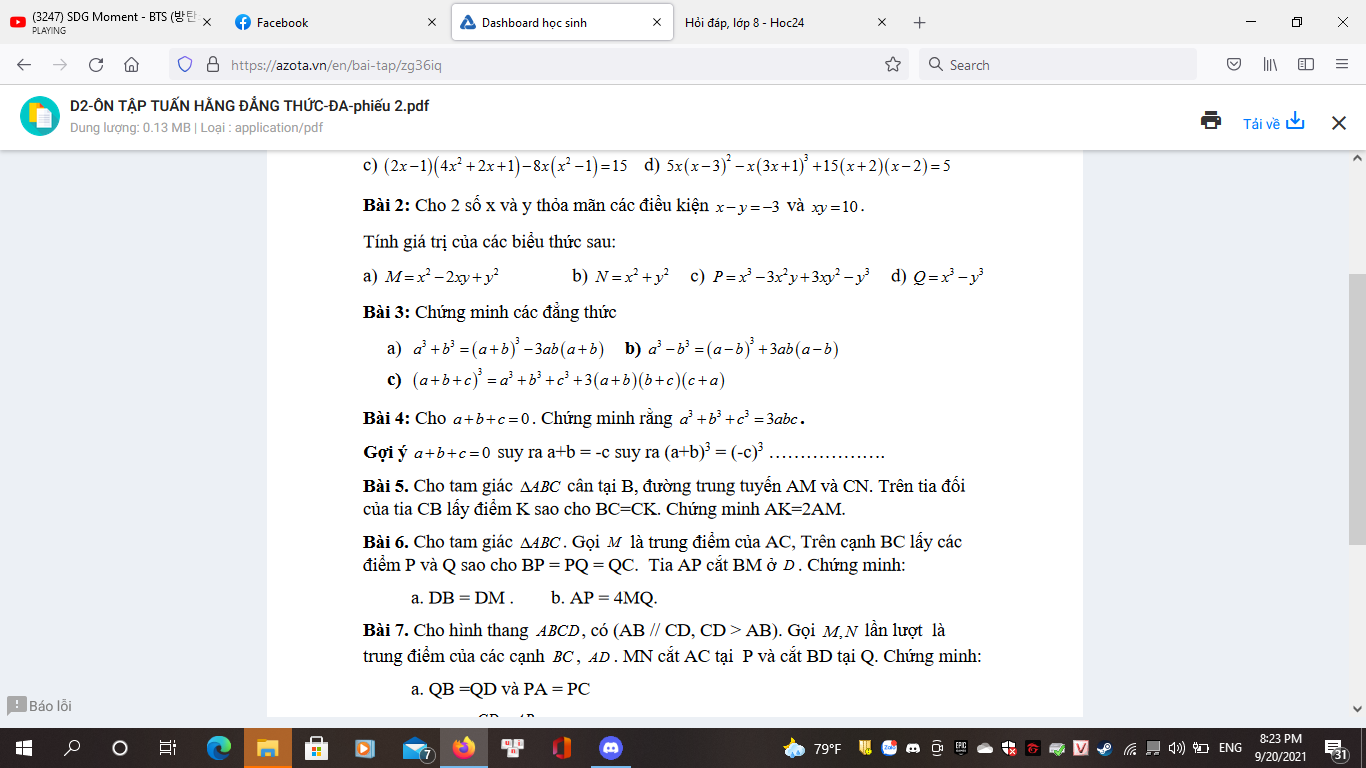 mng giúp mình bài 2 bài 3 bài 4 vs ah
mng giúp mình bài 2 bài 3 bài 4 vs ah

 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk











 giúp mình vs!!!
giúp mình vs!!!


Bài 6:
a: Xét ΔAPC có
M là trung điểm của AC
Q là trung điểm của PC
Do đó: MQ là đường trung bình của ΔAPC
Suy ra: MQ//AP
Xét ΔBMQ có
P là trung điểm của BQ
PD//MQ
Do đó: D là trung điểm của BM
Suy ra: DB=DM