Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2A=1+2+2^2+2^3+...+2^{2022}\)
Lấy 2A - A ta được A = 22022 - 1
22022 - 1 = 22021. 2 -1
Vì 22021 . 2 - 1 < 5.22021
=> A < 5 . 22021

GIÚP MỊ VỚIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

a) A=34+328+3140+...+3550+3700A=34+328+3140+...+3550+3700
A=31.4+34.7+37.10+...+322.25+325.28A=31.4+34.7+37.10+...+322.25+325.28
A=1−14+14−17+

trả lời
tính gì vậy bạn ezz
không phép tính sao làm
hok tốt
Bài 2. Các phép biến đổi và tính toán lũy thừa (tiếp)
Ví dụ: Tính:
.png)

tính chất 2 :
a  m và b
m và b m => (a + b)
 m
m
lưu ý :
- a
 $ m và b
$ m và b m => (a – b)
 m ( với a > b)
m ( với a > b) - a
m và b
 m => (a – b)
m => (a – b) m
m
a  m và b
m và b m và c
m => (a + b + c)
 m
m
Ta có : abc deg = 10000ab + 100cd + eg
= ( 9999ab + ab ) + ( 99cd + cd ) + eg
= ( 9999ab + 99cd ) + ( ab + cd + eg )
= 11( 909ab + 9cd ) + ( ab + cd + eg )
\(\text{Vì }\hept{\begin{cases}11\left(909\overline{ab} + 9\overline{cd}\right)⋮11\\\overline{ab}+\overline{cd}+\overline{eg}⋮11\end{cases}}\)
=> 11( 909ab + 9cd ) + ( ab + cd + eg ) ⋮ 11
=> abc deg ⋮ 11

a. ta có \(1< \left|m-2\right|< 5\Leftrightarrow\orbr{\begin{cases}-5< m-2< -1\\1< m-2< 5\end{cases}\Leftrightarrow\orbr{\begin{cases}-3< m< 1\\3< m< 7\end{cases}}}\)
nên \(m\in\left\{-2;-1;0;4;5;6\right\}\Rightarrow S=12\)
b. ta có \(-5< m+7< 5\Leftrightarrow-12< m< -2\Rightarrow m\in\left\{-11,-10,-9,-8,-7,-6,-5,-4,-3\right\}\)
vậy S=-63

Gọi tập hợp con là A.
\(A=\left\{a,b\right\}\)
Gọi tập hợp con là B.
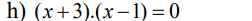
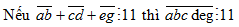
x = -3 và x = 1
\(\Leftrightarrow\left\{{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)