K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DH
1
HT
6 tháng 1 2021
Okie, xinh nên giúp :3 Đùa thui
a/ 5 nguồn mắc nối tiếp \(\left\{{}\begin{matrix}\xi_b=5.\xi=5.4=20\left(V\right)\\r_b=5r=5.0,2=1\left(\Omega\right)\end{matrix}\right.\)
b/ \(R_D=\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right);I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
Đèn sáng bình thường \(\Rightarrow I_2=I_D=I_{dm}=1\left(A\right)\)
\(\left(R_1ntR_B\right)//\left(R_2ntR_D\right)\Rightarrow R_{td}=\dfrac{\left(R_1+R_B\right)\left(R_2+R_D\right)}{R_1+R_B+R_2+R_D}=\dfrac{\left(2+4\right)\left(6+6\right)}{2+4+6+6}=4\left(\Omega\right)\)
c/ \(I=\dfrac{\xi_b}{r_b+R_{td}}=\dfrac{20}{1+4}=4\left(A\right)\)
\(I=I_1+I_2\Rightarrow I_1=I-I_2=4-1=3\left(A\right)\Rightarrow P_1=I_1^2.R_1=3^2.2=18\left(W\right)\)
\(m_{Cu}=\dfrac{A_{Cu}.I_B.t}{F.n}=\dfrac{64.3.\left(32.60+10\right)}{96500.2}=...\left(g\right)\)
TK
16 tháng 12 2021
MCD:R2//R1
\(R=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{18\cdot12}{18+12}=7,2\left(\Omega\right)\)
\(I=\dfrac{E}{R+r}=\dfrac{12}{7,2+0,8}=1,5\left(A\right)\)
\(U_2=U_1=U=R\cdot I=7,2\cdot1,5=10,8\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{10,8}{12}=0,9\left(A\right)\)
Đổi 16 phút 5s=965 s
\(m=\dfrac{1}{F}\cdot\dfrac{A}{n}\cdot I_2\cdot t=\dfrac{1}{96500}\cdot\dfrac{108}{1}\cdot0,9\cdot965=0,972\left(kg\right)\)
NM
1
10 tháng 9 2021
bạn có hỏi mình cái gì đâu mà bọn mình biết trả lời
bạn ph ? thì bọn mình mới biết nên trả lời thế nào
DT
10 tháng 4 2022
a. Độ hội tụ của thấu kính nói trên:
Ta có công thức f = 1/D
=> D = 1/ -f = 1/ -10 = -0,1 m = -10 cm
b. Ảnh cách thấy kính là:
Ta có : \(\dfrac{1}{20}+\dfrac{1}{d'}=\dfrac{1}{-10}\Rightarrow d'=-\dfrac{20}{3}\left(cm\right)\)
c. Sơ đồ tạo ảnh:
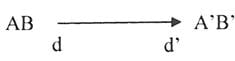
Áp dụng công thức về vị trí ảnh – vật:
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\) suy ra:
\(d'=\dfrac{d.f}{d-f}=\dfrac{20.\left(-10\right)}{20+10}=-\dfrac{20}{3}\left(cm\right)\)
như vậy : d' < 0 nên ảnh thu được là ảnh ảo , cách thấu kính 6,67 cm
Hệ số phóng đại ảnh:
\(k=-\dfrac{d'}{d}=-\dfrac{-\dfrac{20}{3}}{20}=\dfrac{1}{3}\)
Như vậy k > 0 nên ảnh cùng chiều với vật cao bằng một phần ba vật.
d.Chiều cao của ảnh là:
\(k=\dfrac{\overline{A'B'}}{\overline{AB}}=-\dfrac{d'}{d}\Rightarrow\overline{A'B'}=-\dfrac{d'}{d}.\overline{AB}=-\dfrac{-\dfrac{20}{3}}{20}.3=1\left(cm\right)\)