
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)


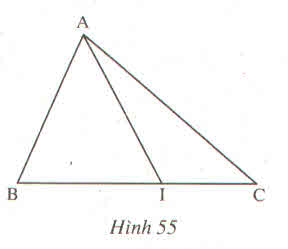
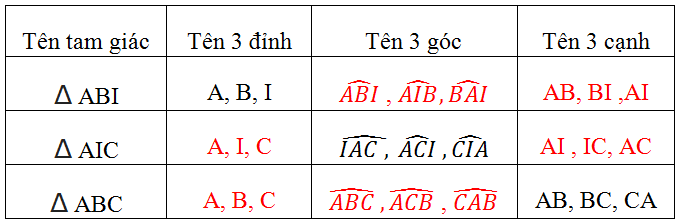
Giải:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |

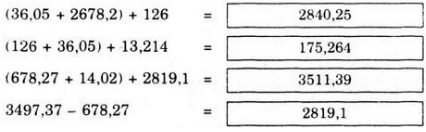
Các kết quả trên đều đúng nên mình điền luôn kết quả nha bạn:
(36,05+2678,2)+126=2840,25.
(126+36,05)+13,214=175,264.
(678,27+14,02)+2819,1=3511,39.
3497,37-678,27=2819,1.
Đó là kết quả của mình có gì sai thì mog pn chỉ ra và giúp mik sửa lỗi nhé!
- Các phép cộng đều cho kết quả đúng.
- Ta có:
(36,05 + 2678,2) + 126
= 36,05 + (2678,2 + 126) (Tính chất kết hợp)
= 36,05 + 2804,2 (theo a)
= 2840,25 (theo c)
(126 + 36,05) + 13,214
= 126 + (36,05 + 13,214) (tính chất kết hợp)
= 126 + 49,264 (theo b)
= 175,264 (theo d)
(678,27 + 14,02) + 2819,1
= (678,27 + 2819,1) + 14,02 (Tính chất giao hoán và kết hợp)
= 3497,37 + 14,02 (theo e)
= 3511,39 (theo g)
3497,37 – 678,27 = 2819,1 (suy từ e)
Vì vậy ta có thể điền số thích hợp và ô trống mà không cần tính toán:

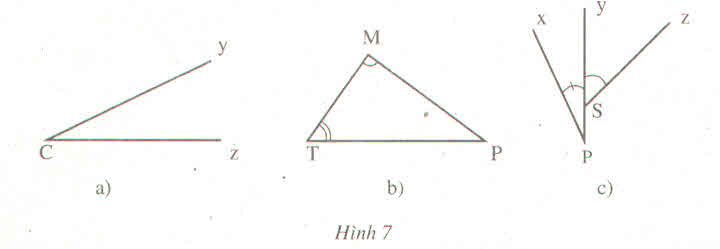
Giải:
|
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|

Gọi thứ tự các ô trong dãy lần lượt là :
01;02;03;04;05;06;07 thì ta có:
01=04=07; 02=05 =176 ; 03=06=324;
Mà 01+02+03=1000 hay 01+176+324=1000
=>01+500=1000 => 01 = 500;
Số thích hợp để điền vào ô thứ nhất là 500...

Bài 3.
Tính số học sinh của lớp 6A.
lớp của 6A trường câụ là bao nhiêu rồi ghi vó là được
chúc bạn học tốt

Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:



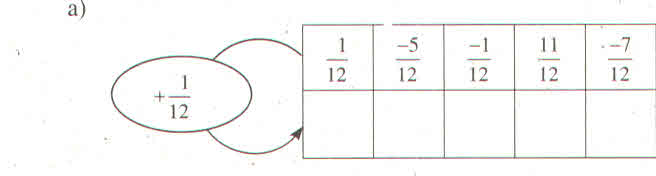
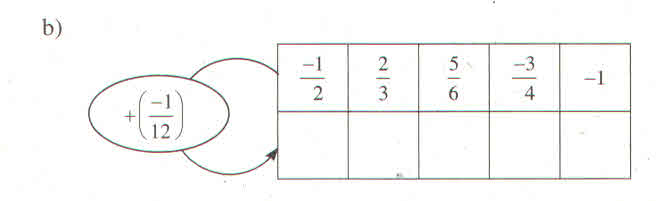









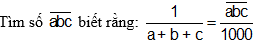

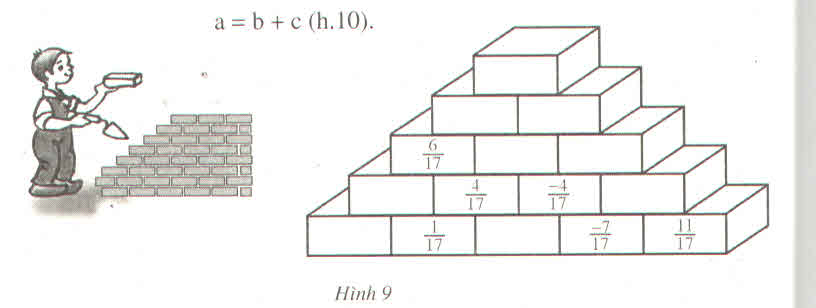
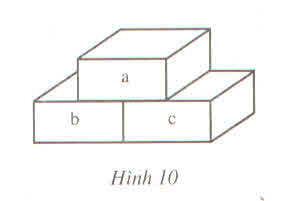
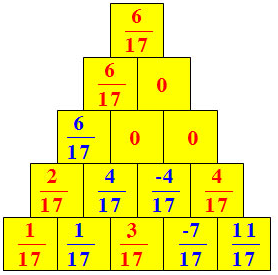
Bài 2:
\(10M=\dfrac{10^{12}+10}{10^{12}+1}=1+\dfrac{9}{10^{12}+1}\)
\(10N=\dfrac{10^{11}+10}{10^{11}+1}=1+\dfrac{9}{10^{11}+1}\)
Ta có: \(10^{12}+1>10^{11}+1\)
=>\(\dfrac{9}{10^{12}+1}< \dfrac{9}{10^{11}+1}\)
=>\(\dfrac{9}{10^{12}+1}+1< \dfrac{9}{10^{11}+1}+1\)
=>10M<10N
=>M<N
Bài 1:
\(A=\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{16}\right)\cdot...\cdot\left(1-\dfrac{1}{900}\right)\)
\(=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{30}\right)\cdot\left(1+\dfrac{1}{2}\right)\cdot\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{30}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{29}{30}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{31}{30}\)
\(=\dfrac{1}{30}\cdot\dfrac{31}{2}=\dfrac{31}{60}\)