
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

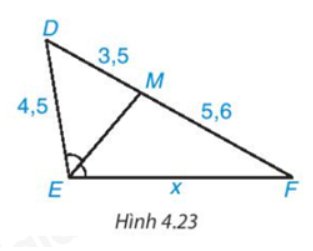
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

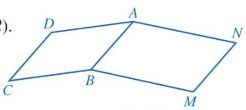
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

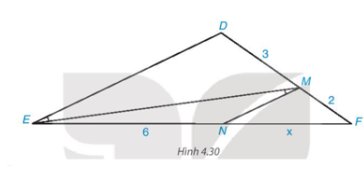
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

Những hình khối có dạng ở hình 11 được gọi là hình chóp tứ giác đều.

• Hình 3.51a)
Tứ giác đã cho có hai đường chéo cắt nhau tại trung điểm của mỗi đường và chúng vuông góc với nhau nên tứ giác đó là hình thoi.
• Gọi tứ giác trong Hình 3.51b) là tứ giác ABCD.
Vì \(\widehat {{B_1}} = \widehat {{D_1}}\) mà hai góc này ở vị trí so le trong nên AB // CD.
Mà AB = CD nên tứ giác ABCD là hình bình hành.
Mặt khác, \(\widehat {{D_1}} = \widehat {{D_2}}\) hay DB là tia phân giác của \(\widehat {A{\rm{D}}C}\)
Khi đó, hình bình hành ABCD có DB là tia phân giác của \(\widehat {A{\rm{D}}C}\).
Do đó tứ giác ABCD là hình thoi.
• Tứ giác trong Hình 3.51c) hai đường chéo vuông góc với nhau và có đường chéo là đường vuông góc của một góc của tứ giác.
Từ đó ta suy ra tứ giác đã cho không phải là hình thoi.
Vậy Hình 3.51a và Hình 3.51b là hình thoi.

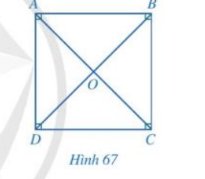
Do tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)








1: AD=8-2=6cm
AD/AB=6/8=3/4
AE/AC=9/12=3/4
=>AD/AB=AE/AC
2: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
3: AI là phân giác
=>IB/IC=AB/AC
=>IB/IC=AD/AE
=>IB*AE=AD*IC