
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)

Câu 6
Thay x=-1 và y=2 vào (d), ta được:
-m+1+2m-3=2
\(\Leftrightarrow m=4\)
Câu 5:
Gọi đths cần tìm là \(y=ax+b\left(a\ne0\right)\)
Vì đt vuông góc với \(y=2x+7\) nên \(2a=-1\Leftrightarrow a=-\dfrac{1}{2}\)
Do đó hệ số góc của đt là \(a=-\dfrac{1}{2}\)

Câu 7:
Thay x=0 và y=9 vào (d), ta được:
-2m-3=9
hay m=-6

\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)

câu 1:
đường thẳng (d) song song với đường thẳng y=3x+1 khi a=3
vậy hệ số góc của đường thẳng (d) song song với đường thẳng y=3x+1 là 3
câu 2:
vì góc tạo bởi đường thẳng (d):y=ax+b(a≠0) với trục Ox là 30o nên
\(a=\tan30^o=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
vậy hệ số góc của đường thẳng (d) tạo với trục Ox là\(\dfrac{\sqrt{3}}{3}\)

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
b: Ta có; ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=13^2-5^2=144\)
=>AM=12(cm)
Xét (O) có
DA,DC là các tiếp tuyến
Do đó: DA=DC và OD là phân giác của góc AOC
Xét (O) có
EB,EC là các tiếp tuyến
Do đó: EB=EC và OE là phân giác của góc BOC
Chu vi tam giác MDE là:
MD+DE+ME
=MD+DC+CE+EM
=MD+DA+ME+EB
=MA+MB
=2MA
=24(cm)
c: Xét (O) có
\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC
\(\widehat{ANC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{MAC}=\widehat{ANC}\)
=>\(\widehat{MAC}=\widehat{MNA}\)
Xét ΔMAC và ΔMNA có
\(\widehat{MAC}=\widehat{MNA}\)
\(\widehat{AMC}\) chung
Do đó: ΔMAC~ΔMNA
=>\(\dfrac{MA}{MN}=\dfrac{MC}{MA}\)
=>\(MA^2=MN\cdot MC\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\)
=>\(MH\cdot MO=MN\cdot MC\)
=>\(\dfrac{MH}{MN}=\dfrac{MC}{MO}\)
Xét ΔMHC và ΔMNO có
\(\dfrac{MH}{MN}=\dfrac{MC}{MO}\)
góc HMC chung
Do đó: ΔMHC~ΔMNO
=>\(\widehat{MHC}=\widehat{MNO}\)
mà \(\widehat{MNO}=\widehat{OCN}\)(ΔOCN cân tại O)
nên \(\widehat{MHC}=\widehat{OCN}\)

Câu 3:
Thay x=-1 và y=0 vào (d), ta được:
-m+2m-1=0
hay m=1

8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
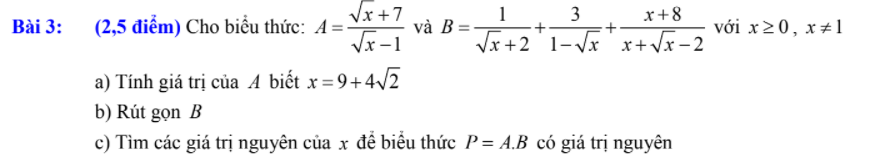 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 



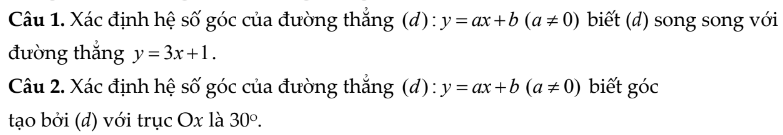

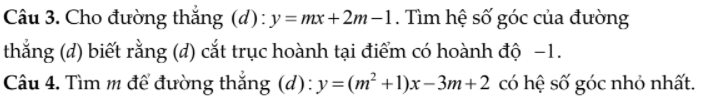 này được
này được 
Đề bài đâu rồi bạn?