
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\)
Do đó: a=30; b=40; c=50

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

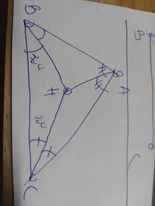
a, \(\dfrac{x}{5}=\dfrac{y}{6};\dfrac{y}{8}=\dfrac{z}{11}\Rightarrow\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{66}=\dfrac{x+y-z}{40+48-66}=\dfrac{44}{22}=2\)
\(\Rightarrow x=80;y=96;z=132\)
b, Ta có : \(3x=8y\Leftrightarrow\dfrac{x}{8}=\dfrac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{8}=\dfrac{y}{3}=\dfrac{x-2y}{8-6}=\dfrac{4}{2}=2\Rightarrow x=16;y=6\)

\(P+Q=\left(5x^3y-2x^3y\right)+\left(2x^2y-3x^2y\right)+\left(-4x^2+4x^2\right)+3xy+12xy-5-\dfrac{1}{2}\)
\(=3x^3y-x^2y+15xy-\dfrac{11}{2}\)

Vẽ lại hình:
Theo hình vẽ, ta có: AH,BH,CH lần lượt là phân giác của góc BAC, góc ABC, góc ACB
BH là phân giác của góc ABC
=>\(\widehat{ABC}=2\cdot\widehat{HBC}=60^0\)
CH là phân giác của góc ACB
=>\(\widehat{ACB}=2\cdot\widehat{HCB}=2\cdot20^0=40^0\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}+60^0+40^0=180^0\)
=>\(\widehat{BAC}=80^0\)
AH là phân giác của góc BAC
=>\(\widehat{BAH}=\widehat{CAH}=\dfrac{80^0}{2}=40^0\)
=>\(x=40^0\)

Tên tam giác là MNP
Tên 3 đỉnh là M,N,P
Tên 3 góc là \(\widehat{mNp};\widehat{nMp};\widehat{nPm}\)
Tên 3 cạnh là MN, NP, MP





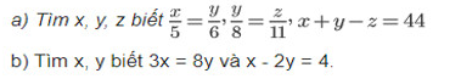


 mn giúp mình với ạ
mn giúp mình với ạ mn giúp mik với ạ
mn giúp mik với ạ 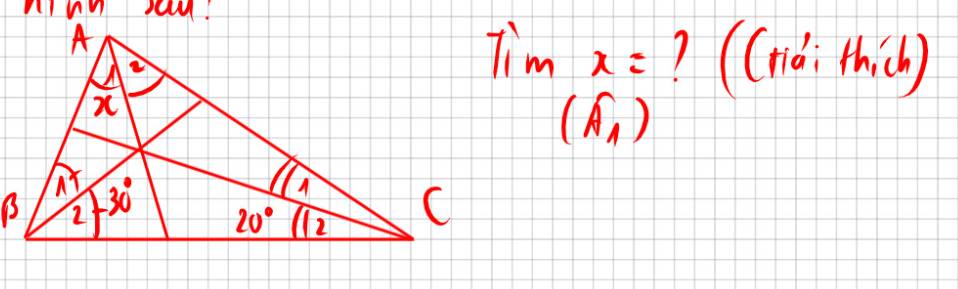
 giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
.... câu hỏi đau
spam à